题目内容
 (2013?南充)如图所示,电源电压恒定,R1=10Ω,滑动变阻器R2的最大阻值为20Ω,当S1、S2均断开,滑片P置于最下端B点时.电流表的示数为0.6A,求:
(2013?南充)如图所示,电源电压恒定,R1=10Ω,滑动变阻器R2的最大阻值为20Ω,当S1、S2均断开,滑片P置于最下端B点时.电流表的示数为0.6A,求:(1)电源电压;
(2)当S1、S2均断开,滑片P置于最上端A点时,在5min内通过R2的电流所产生的热量;
(3)当S1、S2均闭合,滑片P在A、B两端点间时,该电路所消耗的最小功率.
分析:(1)当S1、S2均断开,滑片P置于最下端B点时,电路为R1的简单电路,电流表测电路中的电流,根据欧姆定律求出电源的电压;
(2)当S1、S2均断开,滑片P置于最上端A点时,电阻R1与滑动变阻器的最大阻值串联,根据电阻的串联特点和欧姆定律求出电路中的电流,利用Q=I2Rt求出在5min内通过R2的电流所产生的热量;
(3)当S1、S2均闭合,滑片P在A、B两端点间时,滑动变阻器的PA和PB部分电阻并联,根据电阻的并联特点表示出电路中的总电阻,根据P=
可知,要使电路中的电功率最小应使电路中的总电阻最大,利用数学知识求出电路中的最大电阻即可得出答案.
(2)当S1、S2均断开,滑片P置于最上端A点时,电阻R1与滑动变阻器的最大阻值串联,根据电阻的串联特点和欧姆定律求出电路中的电流,利用Q=I2Rt求出在5min内通过R2的电流所产生的热量;
(3)当S1、S2均闭合,滑片P在A、B两端点间时,滑动变阻器的PA和PB部分电阻并联,根据电阻的并联特点表示出电路中的总电阻,根据P=
| U2 |
| R |
解答:解:(1)当S1、S2均断开,滑片P置于最下端B点时,电路为R1的简单电路,电流表测电路中的电流,
根据欧姆定律可得,电源的电压:
U=I1R1=0.6A×10Ω=6V;
(2)当S1、S2均断开,滑片P置于最上端A点时,电阻R1与滑动变阻器的最大阻值串联,
∵串联电路中总电阻等于各分电阻之和,
∴此时电路中的电流:
I=
=
=0.2A,
在5min内通过R2的电流所产生的热量:
Q2=I2R2t=(0.2A)2×20Ω×5×60s=240J;
(3)当S1、S2均闭合,滑片P在A、B两端点间时,滑动变阻器的PA和PB部分电阻并联,
设RPA=R,则RPB=20Ω-R,
∵并联电路中总电阻的倒数等于各分电阻的倒数之和,
∴R并=
=
=
(-R2+20R),
由二次函数的极值可知,
当R=-
,即R=10Ω时,R并最大,即R并max=
=
=5Ω,
该电路所消耗的最小功率:
Pmin=
=
=7.2W.
答:(1)电源电压为6V;
(2)当S1、S2均断开,滑片P置于最上端A点时,在5min内通过R2的电流所产生的热量为240J;
(3)当S1、S2均闭合,滑片P在A、B两端点间时,该电路所消耗的最小功率为7.2W.
根据欧姆定律可得,电源的电压:
U=I1R1=0.6A×10Ω=6V;
(2)当S1、S2均断开,滑片P置于最上端A点时,电阻R1与滑动变阻器的最大阻值串联,
∵串联电路中总电阻等于各分电阻之和,
∴此时电路中的电流:
I=
| U |
| R1+R2 |
| 6V |
| 10Ω+20Ω |
在5min内通过R2的电流所产生的热量:
Q2=I2R2t=(0.2A)2×20Ω×5×60s=240J;
(3)当S1、S2均闭合,滑片P在A、B两端点间时,滑动变阻器的PA和PB部分电阻并联,
设RPA=R,则RPB=20Ω-R,
∵并联电路中总电阻的倒数等于各分电阻的倒数之和,
∴R并=
| RPARPB |
| RPA+RPB |
| R(20Ω-R) |
| 20Ω |
| 1 |
| 20 |
由二次函数的极值可知,
当R=-
| b |
| 2a |
| R(20Ω-R) |
| 20Ω |
| 10Ω×(20Ω-10Ω) |
| 20Ω |
该电路所消耗的最小功率:
Pmin=
| U2 |
| R并max |
| (6V)2 |
| 5Ω |
答:(1)电源电压为6V;
(2)当S1、S2均断开,滑片P置于最上端A点时,在5min内通过R2的电流所产生的热量为240J;
(3)当S1、S2均闭合,滑片P在A、B两端点间时,该电路所消耗的最小功率为7.2W.
点评:本题考查了串联电路和并联电路的特点以及欧姆定律、电功率公式的应用,关键是开关闭合、断开时电路连接方式的判断和根据二次函数极值的判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?南充)如图所示的电路中,电源电压恒定,R1为定值电阻.闭合开关S,滑动变阻器R2的滑片P由b端移到a端的过程中,下列说法正确的是( )
(2013?南充)如图所示的电路中,电源电压恒定,R1为定值电阻.闭合开关S,滑动变阻器R2的滑片P由b端移到a端的过程中,下列说法正确的是( )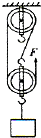 (2013?南充)如图所示,在测量滑轮组的机械效率的实验装置中,动滑轮重0.6N,物重2.4N,不计绳重和各处摩擦,当物体匀速提升时,绳的自由端在竖直方向上的拉力F为
(2013?南充)如图所示,在测量滑轮组的机械效率的实验装置中,动滑轮重0.6N,物重2.4N,不计绳重和各处摩擦,当物体匀速提升时,绳的自由端在竖直方向上的拉力F为 (2013?南充)以下是小明“探究凸透镜成像的规律”的实验过程,请将其补充完整:
(2013?南充)以下是小明“探究凸透镜成像的规律”的实验过程,请将其补充完整: (2013?南充)如图所示,体积为V=200cm3的木块在绳子拉力F=0.8N的作用下完全浸没在水中(g=10N/kg,ρ水=1.0×103kg/m3,绳子重力不计).求:
(2013?南充)如图所示,体积为V=200cm3的木块在绳子拉力F=0.8N的作用下完全浸没在水中(g=10N/kg,ρ水=1.0×103kg/m3,绳子重力不计).求: