题目内容
将额定功率为2W的灯L与一个阻值为4Ω的电阻R串联后接到电压为6V的电源上,小灯泡恰能正常发光,要使电路消耗的电功率较小,小灯泡的额定电压的值和电阻应为( )A.4V,2Ω
B.4V,8Ω
C.2V,2Ω
D.2V,8Ω
【答案】分析:电源的电压一定要使电路消耗的电功率较小则电路中的电流较小,灯泡正常发光时的电压和额定电压相等,根据串联电路的电压特点求出电阻R两端的电压,利用P=UI和欧姆定律分别表示出电路中的电流,利用串联电路的电流特点建立等式,解方程即可求出灯泡额定电压,额定电压大的电流中的电流小,根据P=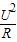 求出灯泡的电阻.
求出灯泡的电阻.
解答:解:灯泡正常发光时的电压为UL,
由P=UI可得,通过灯泡的电流IL=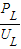 =
=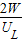 ,
,
∵串联电路中总电压等于各分电压之和,
∴UR=U-UL,
由欧姆定律可得,通过的电流:
IR=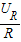 =
=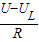 =
=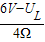 ,
,
∵串联电路中各处的电流相等,
∴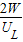 =
=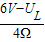 ,
,
整理可得:UL2-6V×UL+2W×4Ω=0,
解得:UL=2V或UL=4V,
∵电路消耗的电功率较小,则电路中的电流较小,灯泡的额定电压较大,
∴UL=4V,
∵P=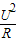 ,
,
∴RL=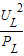 =
=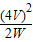 =8Ω.
=8Ω.
故选B.
点评:本题考查了串联电路的特点和欧姆定律、电功率公式的灵活应用,关键是知道要使电路消耗的电功率较小则电路中的电流较小即灯泡的额定电压较大.
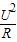 求出灯泡的电阻.
求出灯泡的电阻.解答:解:灯泡正常发光时的电压为UL,
由P=UI可得,通过灯泡的电流IL=
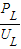 =
=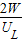 ,
,∵串联电路中总电压等于各分电压之和,
∴UR=U-UL,
由欧姆定律可得,通过的电流:
IR=
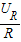 =
=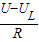 =
=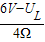 ,
,∵串联电路中各处的电流相等,
∴
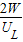 =
=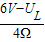 ,
,整理可得:UL2-6V×UL+2W×4Ω=0,
解得:UL=2V或UL=4V,
∵电路消耗的电功率较小,则电路中的电流较小,灯泡的额定电压较大,
∴UL=4V,
∵P=
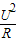 ,
,∴RL=
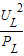 =
=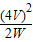 =8Ω.
=8Ω.故选B.
点评:本题考查了串联电路的特点和欧姆定律、电功率公式的灵活应用,关键是知道要使电路消耗的电功率较小则电路中的电流较小即灯泡的额定电压较大.

练习册系列答案
相关题目