题目内容
如图所示,某人用F=40N沿平行于斜面向上的推力匀速将一个G=180N的物体推上高度h=1m、长L=6m的斜面,则该斜面的机械效率为 .在上推过程中所做的额外功为 J;物体所受到的摩擦力为 N.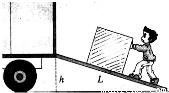
【答案】分析:由推力可求得总功,由重力可求得有用功,则由效率公式可求得机械效率;摩擦力的功即为额外功,则由功的公式可求得摩擦力.
解答:解:人对物体所做的总功W总=FL=40N×6m=240J;
人对物体所做的有用功为W有=Gh=180N×1m=180J
则机械效率η= =75%;
=75%;
额外功W额=W总-W有=240J-180J=60J;
则摩擦力Ff=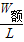 =
=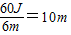 .
.
故答案为:75%,60,10.
点评:斜面模型中人对物体所做的有用功为W有=Gh,总功W总=FL.
解答:解:人对物体所做的总功W总=FL=40N×6m=240J;
人对物体所做的有用功为W有=Gh=180N×1m=180J
则机械效率η=
 =75%;
=75%;额外功W额=W总-W有=240J-180J=60J;
则摩擦力Ff=
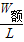 =
=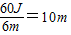 .
.故答案为:75%,60,10.
点评:斜面模型中人对物体所做的有用功为W有=Gh,总功W总=FL.

练习册系列答案
相关题目
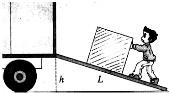 如图所示,某人用F=40N沿平行于斜面向上的推力匀速将一个G=180N的物体推上高度h=1m、长L=6m的斜面,则该斜面的机械效率为
如图所示,某人用F=40N沿平行于斜面向上的推力匀速将一个G=180N的物体推上高度h=1m、长L=6m的斜面,则该斜面的机械效率为