题目内容
质量相等的甲、乙两金属块，其材质不同．将它们放入沸水中，一段时间后温度达到100℃，然后将它们按不同的方式投入一杯冷水中，使冷水升温，第一种方式：先从沸水中取出甲，将其投入冷水，当达到热平衡后将甲从杯中取出，测得水温升高20℃；然后将乙从沸水中取出投入这杯水中，再次达到热平衡，测得水温又升高20℃；第二种方式：先从沸水中取出乙投入冷水，当达到热平衡后将乙从杯中取出；然后将甲从沸水中取出，投入这杯水中，再次达到热平衡．则在第二种方式下，这杯冷水温度升高________40℃（选填“不足”、“超过”或“等于”）．
等于
分析：根据Q放=Q吸和Q=cm（t-t0）列出金属块不同方式下的热量表达式，然后得出关于温度的代数式，即可解答．
解答：设冷水的温度为t0，甲投入冷水后放热Q放=c甲m（100℃-20℃-t0），水吸收的热量为Q吸=c水m水20℃，
∵不考虑热传递过程热量的损失，则有Q放=Q吸，
∴c甲m（100℃-20℃-t0）=c水m水20℃，
即：
=
-----------------------①
乙投入冷水后放热Q放′=C乙m（100℃-20℃-20℃-t0），水吸收的热量仍为Q吸=C水m水20℃，
同理则有：
=
-----------------②
第二种方式：
设乙投入冷水热平衡后，水温为t1，甲投入冷水热平衡后的水温为t2，则有：
c乙m（100℃-t1）=c水m水（t1-t0），
即：=
---------------------③
c甲m（100℃-t2）=c水m水（t2-t1），
即：=
---------------------④
综合①②③④式，解得t2-t0=40℃
故答案为：等于．
点评：本题需要假设的量和列出的计算等式有点多，需要认真分析需要假设的量，由于冷水的初温设为t0，计算过程比较繁杂，如果我们把t0设为0℃，则解题过程大大地简化了．
分析：根据Q放=Q吸和Q=cm（t-t0）列出金属块不同方式下的热量表达式，然后得出关于温度的代数式，即可解答．
解答：设冷水的温度为t0，甲投入冷水后放热Q放=c甲m（100℃-20℃-t0），水吸收的热量为Q吸=c水m水20℃，
∵不考虑热传递过程热量的损失，则有Q放=Q吸，
∴c甲m（100℃-20℃-t0）=c水m水20℃，
即：
=-----------------------①乙投入冷水后放热Q放′=C乙m（100℃-20℃-20℃-t0），水吸收的热量仍为Q吸=C水m水20℃，
同理则有：
=-----------------②第二种方式：
设乙投入冷水热平衡后，水温为t1，甲投入冷水热平衡后的水温为t2，则有：
c乙m（100℃-t1）=c水m水（t1-t0），
即：
=---------------------③c甲m（100℃-t2）=c水m水（t2-t1），
即：
=---------------------④综合①②③④式，解得t2-t0=40℃
故答案为：等于．
点评：本题需要假设的量和列出的计算等式有点多，需要认真分析需要假设的量，由于冷水的初温设为t0，计算过程比较繁杂，如果我们把t0设为0℃，则解题过程大大地简化了．
练习册系列答案
相关题目
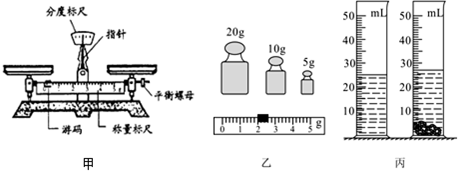
用质量相等的金条和银条做成两个工艺品（没损耗），把它们分别放在甲、乙量筒中的情景如图所示．以下判断正确的是（ ）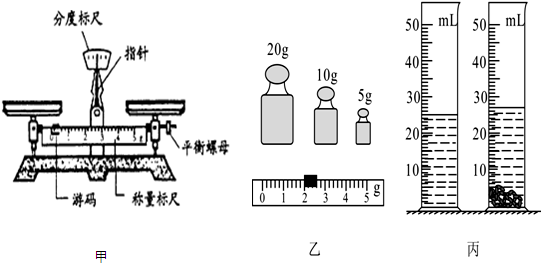
通过计算，可以判定这款手链产品_______（“是”或“不是”）纯金的。
用质量相等的金条和银条做成两个工艺品（没损耗），把它们分别放在甲、乙量筒中的情景如图所示．以下判断正确的是