题目内容
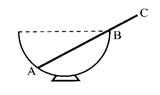
如图16所示,直径为36cm的半球形碗固定在水平面上,碗的端口水平。一根密度分布均匀、长度为47cm的光滑杆ABC搁置在半球碗上,碗的厚度不计,杆平衡时碗内部分AB段与碗外部分BC段的长度之比为( )

| A.38:9 | B.35:12 | C.32:15 | D.27:20 |
C
试题分析:光滑杆在碗中的受力情况如图所示,设杆的重为G,AB的长为x,碗的半径为R,D为杆的中点,AD=
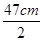 ,A 端受到的作用力与杆间的夹角为θ,则cosθ=
,A 端受到的作用力与杆间的夹角为θ,则cosθ=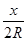 ,
,又因为杆是平衡的,即以A为支点杆遵循杠杆的平衡,故F1×x=G×AD×cosθ;
以B为支点杆也遵循杠杆的平衡,故F2×x×sinθ=G×BD×cosθ;
联立以上两式得:
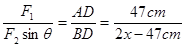
对杆进行受力分析得,在沿杆的方向是平衡的,则F2cosθ=Gsinθ;在垂直杆的方向也是平衡的,即F2sinθ+F1=Gcosθ;再联立 以上式子得:
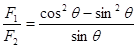
所以可得出
 ,将cosθ=
,将cosθ=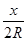 代入可整理得:4x2-47x-8R2=0,由于R=18cm,故解之得x=35cm,则BC=47cm-35cm=12cm,所以AB:BC=35:12,C是正确的。
代入可整理得:4x2-47x-8R2=0,由于R=18cm,故解之得x=35cm,则BC=47cm-35cm=12cm,所以AB:BC=35:12,C是正确的。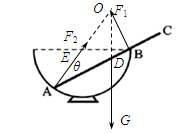

练习册系列答案
相关题目