题目内容
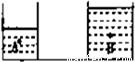
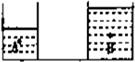 如图,相同的两个容器中分别盛有质量相等的水和酒精,液体内部A,B两点在同一水平高度,这两点的压强分别为PA和PB,则
如图,相同的两个容器中分别盛有质量相等的水和酒精,液体内部A,B两点在同一水平高度,这两点的压强分别为PA和PB,则
- A.PA>PB
- B.PA=PB
- C.PA<PB
- D.无法判断
C
分析:根据题意“相同的两个容器中分别盛有质量相等的水和酒精,液体内部A,B两点在同一水平高度,”即H相同,设A、B两点的深度为hA、hB,根据液体压强的计算公式P=ρgh,而ρ水大于ρ酒精,故有此不能确定PA和PB的关系,应另辟思路.
采用切割法,将A、B以下部分“切割”,对切割部分有VAH=VBH.又因为ρ水>ρ酒精,所以可以得出被切割部分的质量mAH>mBH,然后可计算出切割后余下的液体重,由此可得PA,同理可得PB,然后即可得出答案.
解答:设A、B两点的深度为hA、hB,根据液体压强的计算公式PA=ρ水ghA,PB=ρ酒精ghB,而ρ水大于ρ酒精,故有此不能确定PA和PB的关系,应另辟思路.
采用切割法,将A、B以下部分“切割”,对切割部分有VAH=VBH.
又因为ρ水>ρ酒精,
由m=ρV可知,被切割部分的质量mAH>mBH,则GAH>GBH,
切割后余下的液体重为G液′=G液总-G切,
所以PA=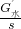 =
=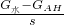 …①
…①
PB= =
=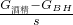 …②,
…②,
由题意知G水=G酒精,比较①与②,可得PA<PB.

故选C.
点评:本题考查容器底部所受液体压强的计算,最关键的是知道液体中某一点的深度指的是这一点到液面的垂直距离,而不是距离容器底的距离,这是最容易出错的.而此题中的“液体内部A,B两点在同一水平高度,”学生容易看成是液面到A、B的垂直距离,容易错选B选项,因此做题时一定要认真审题.
分析:根据题意“相同的两个容器中分别盛有质量相等的水和酒精,液体内部A,B两点在同一水平高度,”即H相同,设A、B两点的深度为hA、hB,根据液体压强的计算公式P=ρgh,而ρ水大于ρ酒精,故有此不能确定PA和PB的关系,应另辟思路.
采用切割法,将A、B以下部分“切割”,对切割部分有VAH=VBH.又因为ρ水>ρ酒精,所以可以得出被切割部分的质量mAH>mBH,然后可计算出切割后余下的液体重,由此可得PA,同理可得PB,然后即可得出答案.
解答:设A、B两点的深度为hA、hB,根据液体压强的计算公式PA=ρ水ghA,PB=ρ酒精ghB,而ρ水大于ρ酒精,故有此不能确定PA和PB的关系,应另辟思路.
采用切割法,将A、B以下部分“切割”,对切割部分有VAH=VBH.
又因为ρ水>ρ酒精,
由m=ρV可知,被切割部分的质量mAH>mBH,则GAH>GBH,
切割后余下的液体重为G液′=G液总-G切,
所以PA=
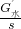 =
=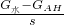 …①
…①PB=
 =
=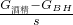 …②,
…②,由题意知G水=G酒精,比较①与②,可得PA<PB.

故选C.
点评:本题考查容器底部所受液体压强的计算,最关键的是知道液体中某一点的深度指的是这一点到液面的垂直距离,而不是距离容器底的距离,这是最容易出错的.而此题中的“液体内部A,B两点在同一水平高度,”学生容易看成是液面到A、B的垂直距离,容易错选B选项,因此做题时一定要认真审题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
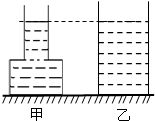 (2012?昭通)如图所示的两个容器放在水平桌面上,它们的质量和底面积均相同,容器中分别装有甲、乙两种液体且液面在同一高度.若容器对桌面的压强相等,则两种液体对容器底部的压强( )
(2012?昭通)如图所示的两个容器放在水平桌面上,它们的质量和底面积均相同,容器中分别装有甲、乙两种液体且液面在同一高度.若容器对桌面的压强相等,则两种液体对容器底部的压强( ) 如图所示的两个容器中盛有同种相同质量的液体,容器底受到的压强较大的是
如图所示的两个容器中盛有同种相同质量的液体,容器底受到的压强较大的是 如图,相同的两个容器中分别盛有质量相等的水和酒精,液体内部A,B两点在同一水平高度,这两点的压强分别为PA和PB,则( )
如图,相同的两个容器中分别盛有质量相等的水和酒精,液体内部A,B两点在同一水平高度,这两点的压强分别为PA和PB,则( )