题目内容
【题目】A、B、C是由密度为ρ=3.0×103kg/m3的某种合金制成的三个实心球.A球的质量mA=90g;甲和乙是两个完全相同的木块,其质量m甲=m乙=340g;若把B和C挂在轻质杠杆两端,平衡时如图1所示,其中MO:ON=3:1.若用细线把球和木块系住,放入底面积为400cm2的圆柱形容器中,在水中静止时如图2所示.在图2中,甲有一半体积露出水面,乙浸没水中(水的密度为1.0×103kg/m3 , g取10N/kg,杠杆、滑轮与细线的质量以及它们之间的摩擦忽略不计). 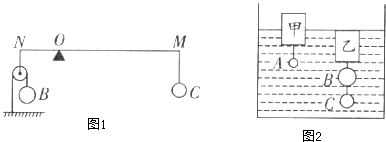
(1)甲木块的体积是多少?
(2)求B和C的质量各为多少kg?
(3)若将A球与甲相连的细线以及C球与B球相连的细线都剪断,甲和乙重新静止后,水对容器底部的压强变化了多少?
【答案】
(1)G甲=G乙=m甲g=340×10﹣3kg×10N/kg=3.4N
GA=mAg=90×10﹣3kg×10N/kg=0.9N
VA= ![]() =
= ![]() =0.3×10﹣4m3
=0.3×10﹣4m3
将甲、A看做一个整体,因为漂浮,则:ρ水g( ![]() +VA)=G甲+GA
+VA)=G甲+GA
即:1.0×103kg/m3×10N/kg×( ![]() +0.3×10﹣4m3)=3.4N+0.9N
+0.3×10﹣4m3)=3.4N+0.9N
解得:V甲=8×10﹣4m3
答:甲木块的体积是8×10﹣4m3
(2)由图1知,杠杆杠杆平衡条件:
2mBgON=mCgOM
∵MO:ON=3:1
∴2mB×ON=mC×3ON
则mB=1.5mC
由图2知,乙、B、C悬浮在水中,将乙、B、C看做一个整体,则:
ρ水g(V乙+VB+VC)=G乙+GB+GC
即:1.0×103kg/m3×10N/kg×(8.0×10﹣4m3+ ![]() +
+ ![]() )=3.4N+mB×10N/kg+mC×10N/kg
)=3.4N+mB×10N/kg+mC×10N/kg
则:1.0×103kg/m3×(8.0×10﹣4m3+ ![]() +
+ ![]() )=0.34kg+1.5mC+mC
)=0.34kg+1.5mC+mC
解得:mC=0.276kg
mB=1.5mC=1.5×0.276kg=0.414kg
答:B的质量为0.414kg;C的质量为0.276kg
(3)把甲、乙、A、B、C看做一个整体,原来都漂浮,浮力等于所有物体的总重力;
若将线剪断,则甲、乙、B漂浮在水面,A、C沉入水底,此时整体受到的浮力减小,且
VA= ![]() =
= ![]() =3×10﹣5m3;VC=
=3×10﹣5m3;VC= ![]() =
= ![]() =9.2×10﹣5m3;
=9.2×10﹣5m3;
△F浮=(GA+GC)﹣ρ水g(VA+VC)
=(0.09kg+0.276kg)×10N/kg﹣1.0×103kg/m3×10N/kg×(3×10﹣5m3+9.2×10﹣5m3)
=3.66N﹣1.22N
=2.44N;
则△V排= ![]() =
= ![]() =2.44×10﹣4m3;
=2.44×10﹣4m3;
则△h= ![]() =
= ![]() =0.0061m
=0.0061m
由于液面下降,所以压强减小,则:△p=ρ水g△h=1.0×103kg/mspan>3×10N/kg×0.0061m=61Pa
答:甲和乙重新静止后,水对容器底部的压强减小了61Pa
【解析】(1)把甲和A看做一个整体,根据物体漂浮时,浮力与重力相等进行分析;(2)根据杠杆平衡条件结合动滑轮的特点列出关系式;根据图2,将乙、B、C看做一个整体,根据悬浮时浮力与重力相等,列出关系式;将两个关系式联立并代入已知条件便可求出;(3)求出甲、乙漂浮在水面上时排开水的体积与原来相比,结合容器底的底面积求出水的液面高度的变化,根据公式p=ρ液gh求出压强的变化.
【考点精析】关于本题考查的杠杆的平衡条件和滑轮组及其工作特点,需要了解杠杆平衡:杠杆在动力和阻力的作用下静止或匀速转动时,称为杠杆平衡.杠杆平衡是力和力臂乘积的平衡,而不是力的平衡.杠杆平衡的条件:动力 ×动力臂 = 阻力 ×阻力臂即:F1 L1 = F2 L2可变形为 :F1 / F2 = L1 / L2;滑轮组的工作特点: (1)可以改变力的方向,也可以不改变.(2)重物和动滑轮的重力有几段绳承担,所用的拉力就是它们的总重力的几分之一.拉力作用点移动的距离就是重物移动距离的几倍才能得出正确答案.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】某实验小组在使用如图所示装置来做“探究水的沸腾”的实验中,用酒精灯给水加热至90℃时开始记时,每隔1min记录一次温度,记录数据见下表: 
时间/min | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
温度/℃ | 90 | 92 | 94 | 96 | 98 | 99 | 99 | 99 | 99 | 99 | 99 |
(1)实验小组测得水的沸点是℃;从开始记时到水沸腾经历的时间为min.
(2)水沸腾时大量气泡上升,气泡体积 , 到水面破裂;在沸腾过程中,水继续吸热,温度 . (选填“变大”、“变小”或“不变”)





