题目内容
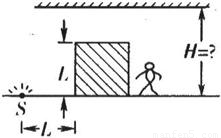
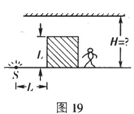
 如图所示,某房间水平地面上有一点光源S,距离点光源为L的地面上,放有一边长为L且不透光的立方体物块,并且正好挡住了房间内某同学的视线.该同学只好通过安置在天花板上的平面镜来观察光源的像,则平面镜离地面的高度不得低于
如图所示,某房间水平地面上有一点光源S,距离点光源为L的地面上,放有一边长为L且不透光的立方体物块,并且正好挡住了房间内某同学的视线.该同学只好通过安置在天花板上的平面镜来观察光源的像,则平面镜离地面的高度不得低于
- A.4L/3
- B.3L/2
- C.5L/3
- D.2L
B
分析:连接S与立方体的左顶点并延长.根据反射定律,则过立方体的右顶点作斜率相同方向相反的线与刚才的线相交 因为立方体边长为L,S点距立方体长也为L,然后利用几何知识解答即可.
解答:连接S与立方体的左顶点并延长,连接某同学的视线与立方体的右顶点并延长,交平面镜与一点O,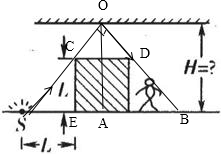
∵立方体物块的边长为L,SE=L,
∴△SEC、SOA为等腰直角三角形,
∴△SOB也为等腰直角三角形,
∵OA⊥SB,∴SA=AB,
∴AE= L,
L,
则H=OA=SA=SE+AE=L+ L=
L=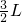 .
.
故选B.
点评:知道点光源的发出的光经平面镜反射后,反射光线的反向延长线过像点,然后根据几何知识求得AE= L是解答此题的关键,此题有一定的拔高难度,对学生的要求比较高,要求学生解答此题时应具备较好的数学基础.
L是解答此题的关键,此题有一定的拔高难度,对学生的要求比较高,要求学生解答此题时应具备较好的数学基础.
分析:连接S与立方体的左顶点并延长.根据反射定律,则过立方体的右顶点作斜率相同方向相反的线与刚才的线相交 因为立方体边长为L,S点距立方体长也为L,然后利用几何知识解答即可.
解答:连接S与立方体的左顶点并延长,连接某同学的视线与立方体的右顶点并延长,交平面镜与一点O,

∵立方体物块的边长为L,SE=L,
∴△SEC、SOA为等腰直角三角形,
∴△SOB也为等腰直角三角形,
∵OA⊥SB,∴SA=AB,
∴AE=
 L,
L,则H=OA=SA=SE+AE=L+
 L=
L=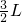 .
.故选B.
点评:知道点光源的发出的光经平面镜反射后,反射光线的反向延长线过像点,然后根据几何知识求得AE=
 L是解答此题的关键,此题有一定的拔高难度,对学生的要求比较高,要求学生解答此题时应具备较好的数学基础.
L是解答此题的关键,此题有一定的拔高难度,对学生的要求比较高,要求学生解答此题时应具备较好的数学基础. 
练习册系列答案
相关题目
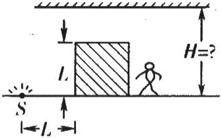 如图所示,某房间水平地面上有一点光源S,距离点光源为L的地面上,放有一边长为L且不透光的立方体物块,并且正好挡住了房间内某同学的视线.该同学只好通过安置在天花板上的平面镜来观察光源的像,则平面镜离地面的高度不得低于( )
如图所示,某房间水平地面上有一点光源S,距离点光源为L的地面上,放有一边长为L且不透光的立方体物块,并且正好挡住了房间内某同学的视线.该同学只好通过安置在天花板上的平面镜来观察光源的像,则平面镜离地面的高度不得低于( )