题目内容
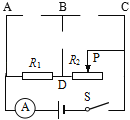
【题目】在图(a)所示的电路中,电源电压为6伏且不变.
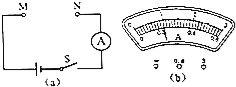
①将定值电阻R1接入M、N接线柱,闭合电键S后电流表A的示数为0.4安.求:
(a)电阻R1的阻值;
(b)求电阻R1的电功率P1.
②现将标有“10Ω 1A”字样的滑动变阻器R2与R1以某种最基本的连接方式接入M、N接线柱,闭合电键S,移动变阻器R2的滑片,能使电流表的指针到达图(b)所示位置.
(a)请通过计算判断电阻R1与变阻器R2的连接方式;
(b)在电路元件安全工作的条件下,移动变阻器R2滑片,求电流表示数的最大变化量△I.
【答案】①(a)电阻R1的阻值为15Ω;(b)电阻R1的电功率为2.4W.
②(a)电阻R1与变阻器R2的连接方式为并联;(b)电流表示数的最大变化量△I为0.4A.
【解析】试题分析:①知道电源的电压和电路中的电流,根据欧姆定律求出电阻R1的阻值,再根据P=UI求出电阻R1的电功率;
②R1与R2的连接方式要么是串联、要么是并联,若两电阻串联,当滑动变阻器接入电路中的电阻最大时电路中的电流最小,根据电阻的串联和欧姆定律求出电路中的最小电流,然后与电流表可能的示数相比较确定电路的连接方式为并联,根据并联电路的电压特点和欧姆定律求出通过R2的最小电流,根据滑动变阻器的铭牌可知允许通过的最大电流,然后求出电流表示数的最大变化量.
解:①将定值电阻R1接入M、N接线柱时,电路为R1的简单电路,
(a)由I=![]() 可得,电阻R1的阻值:
可得,电阻R1的阻值:
R1=![]() =
=![]() =15Ω;
=15Ω;
(b)电阻R1的电功率:
P1=UI=6V×0.4A=2.4W;
②R1与R2的连接方式要么是串联、要么是并联,
若两电阻串联,当滑动变阻器接入电路中的电阻最大时电路中的电流最小,
因串联电路中总电阻等于各分电阻之和,
所以,电路中的最小电流:
I=![]() =
=![]() =0.24A,
=0.24A,
即电路中的电流变化范围0.24A~0.4A,
而图(b)中电流表的示数为0.2A或1A,故R1与R2的连接方式应为并联,
因并联电路中各支路独立工作、互不影响,
所以,通过R1的电流不变,
当R2接入电路中的电阻最大时,电流表的示数最小,
因并联电路中各支路两端的电压相等,
所以,通过R2的最小电流:
I2小=![]() =
=![]() =0.6A,
=0.6A,
因并联电路中干路电流等于各支路电流之和,
所以,电流表的最小示数:
I小=I1+I2小=0.4A+0.6A=1A,
滑动变阻器允许通过的最大电流为1A,则电流表的最大示数:
I大=I1+I2大=0.4A+1A=1.4A,
则电流表示数的最大变化量:
△I=I大﹣I小=1.4A﹣1A=0.4A.
答:①(a)电阻R1的阻值为15Ω;(b)电阻R1的电功率为2.4W.
②(a)电阻R1与变阻器R2的连接方式为并联;(b)电流表示数的最大变化量△I为0.4A.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案