题目内容
【题目】如图所示,质量不计的光滑木板AB长1.2m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是9N.求:

(1)请在图中画出A段细绳拉力的力臂;
(2)重物G的重力
(3)在O点的正上方放一质量为0.6kg的小球,若小球以15cm/s的速度由O点沿木板向A端匀速运动,问小球至少运动多长时间细绳的拉力减小到零.(取g=10N/kg,绳的重力不计)
故
【答案】(1如上图所示、(2)9N (3)4s
【解析】解答:(1)A点所受力的方向与细绳的方向一致。力臂是指从支点到力的作用线的距离。所以从支点O向绳子做垂线段,所做垂线段即为拉力的力臂L1,如图所示;
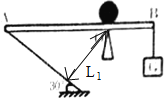
(2)细绳于水平地面成30夹角,因为木板在水平位置平衡(即木板雨水平面平行),所以细绳与木板也成30夹角。根据直角三角形的知识可知L1=1/2OA,OB为G的力臂,
根据杠杆平衡条件得:F绳×L1=G×BO,
即 F绳×1/2AO=G×BO
即:9N×1/2(1.2m0.4m)=G×0.4m,
解:G=9N;
(3)球的重力G球=m球g=0.6kg×10N/kg=6N,
当绳子拉力为0时,设球离O点距离为L,
则根据杠杆平衡条件得:G球×L =G×BO,
即:6N×L =9N×0.4m,
所以L =0.6m=60cm,
小球运动的时间:t=L/ v=60cm/15cm/s=4s.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目