��Ŀ����
����Ŀ����ͼ��ʾ���������ƵĹ⻬ľ��AB��1.2m�����ƹ̶���Oת������O��0.2m��B�˹�һ����G�����A����һ����ˮƽ�����30��нǵ�ϸ����ס��ľ����ˮƽλ��ƽ��ʱ����������6N��Ȼ����O������Ϸ���һ����Ϊ0.3kg��С����С����25cm/s���ٶ���O����ľ����A�������˶�����С�������˶��ʱ��ϸ����������С���㡣(ȡg=10N/kg��������������)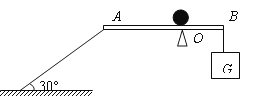
���𰸡��⣺�������������ۣ���ͼ��ʾ��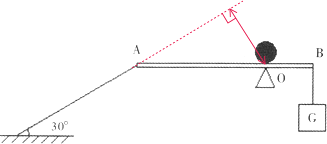
�ɸܸ�ƽ�������ã�F����AOsin30��=G��BO��
����6N��(1.2m��0.2m)=G��0.2m����ã�G=15N��
�������G��=m��g=0.3kg��10N/kg=3N��
����������Ϊ0ʱ��������O�����ΪL�� ��
�ɸܸ�ƽ�������ã�G����L��=G��BO��
����3N��L��=15N��0.2m��
��ã�L��=1m=100cm��
���ٶȹ�ʽ�� ![]() ��֪��
��֪��
����˶�ʱ�䣺 ![]() ��
��
�����������ոܸ�ƽ��������Ӧ�á�����ƽ��������

��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ