题目内容
在某工地上,工人师傅用滑轮组起吊重为600N的物体,他站在地面上用200N、的力往下拉绳,使物体匀速上升3m,滑轮组工作时的效率为75%.(1)求滑轮组提升重物所做的有用功和该工人的拉力所做的总功;
(2)求该滑轮组中吊起动滑轮的绳子股数n,并画出这个滑轮组的示意图.
分析:(1)知道物体重和被提升的高度,利用W=Gh求有用功;因为s不知,人做的总功不能用W=Fs求,可由η=
求解;
(2)物体被n股绳子承担,拉力移动的距离就是物体和动滑轮移动距离的n倍,根据η=
=
求n的大小;然后根据奇动偶定的原则(n为奇数从动滑轮绕起、n为偶数从定滑轮绕起)画出绕法.
| W有 |
| W总 |
(2)物体被n股绳子承担,拉力移动的距离就是物体和动滑轮移动距离的n倍,根据η=
| W有 |
| W总 |
| Gh |
| Fs |
解答:解:(1)人做的有用功: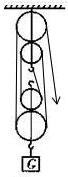
W有=Gh=600N×3m=1800J,
∵η=
,
∴人做的总功:
W总=
=
=2400J;
(2)设有n段绳子承担,则:
η=
=
=
=75%,
解得:s=4h,
∴n=4;
由题意知,人要站在地上往下拉,即要改变力的方向,因此需要两个动滑轮、两个动滑轮;先从定滑轮的挂钩开始,然后依次绕线,如图所示:
答:(1)滑轮组提升重物所做的有用功为1800J,该工人的拉力所做的总功为2400J;
(2)该滑轮组中吊起动滑轮的绳子股数n为4,滑轮组的示意图如图所示.

W有=Gh=600N×3m=1800J,
∵η=
| W有 |
| W总 |
∴人做的总功:
W总=
| W有 |
| η |
| 1800J |
| 75% |
(2)设有n段绳子承担,则:
η=
| W有 |
| W总 |
| Gh |
| Fs |
| 600N×h |
| 200N×s |
解得:s=4h,
∴n=4;
由题意知,人要站在地上往下拉,即要改变力的方向,因此需要两个动滑轮、两个动滑轮;先从定滑轮的挂钩开始,然后依次绕线,如图所示:
答:(1)滑轮组提升重物所做的有用功为1800J,该工人的拉力所做的总功为2400J;
(2)该滑轮组中吊起动滑轮的绳子股数n为4,滑轮组的示意图如图所示.
点评:本题考查的知识点多,用到的公式多,难点是n的计算;滑轮组的绕法采用奇动偶定的原则(n为奇数从动滑轮绕起、n为偶数从定滑轮绕起)的原则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
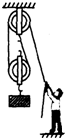 (2010?常德)如图所示,在某工地上,工人师傅用滑轮组匀速吊起重为400N的物体,他站在地面上用250N的拉力向下拉绳,将物体提升3m.求:
(2010?常德)如图所示,在某工地上,工人师傅用滑轮组匀速吊起重为400N的物体,他站在地面上用250N的拉力向下拉绳,将物体提升3m.求: