题目内容
某物体从A到B,后 的路程的速度是前
的路程的速度是前 的路程的速度的
的路程的速度的 .如果整个的路程中的平均速度是18千米/小时,则它在前后两部分路程的速度分别为
.如果整个的路程中的平均速度是18千米/小时,则它在前后两部分路程的速度分别为
- A.24千米/小时,8千米/小时
- B.18千米/小时,6千米/小时
- C.30千米/小时,10千米/小时
- D.36千米/小时,12千米/小时
C
分析:解答本题我们需要分别设两个物理量:设整个路程为s,则前 的路程为
的路程为 s,后
s,后 的路程为
的路程为 s;设前
s;设前 路程的速度为v,则后
路程的速度为v,则后 路程的速度是
路程的速度是 v.由此我们就可以分别得出前
v.由此我们就可以分别得出前 路程的时间表达式和后
路程的时间表达式和后 路程的时间表达式,从而得出总时间,这样我们就可以用总路程、总时间和全程的平均速度建立一个方程,解答此方程就可以算出物体在前后两部分路程的速度.
路程的时间表达式,从而得出总时间,这样我们就可以用总路程、总时间和全程的平均速度建立一个方程,解答此方程就可以算出物体在前后两部分路程的速度.
解答:设整个路程为s,则前 的路程为
的路程为 s,后
s,后 的路程为
的路程为 s;设前
s;设前 路程的速度为v,则后
路程的速度为v,则后 路程的速度是
路程的速度是 v,
v,
物体在前一部分路程所用的时间:t1= ,
,
物体在后一部分路程所用的时间:t2= =
=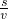 ,
,
则物体在整个路程的运动时间:t=t1+t2= +
+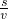 =
= =
= ,
,
由v= 得:
得: =18千米/小时,
=18千米/小时,
解得:v=30千米/小时,则 v=10千米/小时.
v=10千米/小时.
故选 C.
点评:解答本题的关键是要会设物理量并建立方程,从而进行求解.计算平均速度一定要指明路程(或时间),一定要用该路程除以该路程所用的时间.
分析:解答本题我们需要分别设两个物理量:设整个路程为s,则前
 的路程为
的路程为 s,后
s,后 的路程为
的路程为 s;设前
s;设前 路程的速度为v,则后
路程的速度为v,则后 路程的速度是
路程的速度是 v.由此我们就可以分别得出前
v.由此我们就可以分别得出前 路程的时间表达式和后
路程的时间表达式和后 路程的时间表达式,从而得出总时间,这样我们就可以用总路程、总时间和全程的平均速度建立一个方程,解答此方程就可以算出物体在前后两部分路程的速度.
路程的时间表达式,从而得出总时间,这样我们就可以用总路程、总时间和全程的平均速度建立一个方程,解答此方程就可以算出物体在前后两部分路程的速度.解答:设整个路程为s,则前
 的路程为
的路程为 s,后
s,后 的路程为
的路程为 s;设前
s;设前 路程的速度为v,则后
路程的速度为v,则后 路程的速度是
路程的速度是 v,
v,物体在前一部分路程所用的时间:t1=
 ,
,物体在后一部分路程所用的时间:t2=
 =
=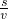 ,
,则物体在整个路程的运动时间:t=t1+t2=
 +
+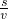 =
= =
= ,
,由v=
 得:
得: =18千米/小时,
=18千米/小时,解得:v=30千米/小时,则
 v=10千米/小时.
v=10千米/小时.故选 C.
点评:解答本题的关键是要会设物理量并建立方程,从而进行求解.计算平均速度一定要指明路程(或时间),一定要用该路程除以该路程所用的时间.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 路程速度是前
路程速度是前 路程速度的
路程速度的 的路程的速度是前
的路程的速度是前 的路程的速度的
的路程的速度的 .如果整个的路程中的平均速度是18千米/小时,则它在前后两部分路程的速度分别为( )
.如果整个的路程中的平均速度是18千米/小时,则它在前后两部分路程的速度分别为( )