题目内容
（本题6分）某初级中学的同学在学习了“科学探究的方法”和“密度”知识后，产生了探究马铃薯（俗称洋芋）密度的兴趣。他们经过讨论提出如下猜想：
A．洋芋的密度与品种有关；
B．洋芋的密度与质量有关；
C．洋芋的密度与成熟度有关。
(1)请你根据生活经验，再提出一个猜想： 。
(2)为了验证猜想A，需要控制洋芋的 和 ，为此他们从市场上选购了“小紫芋”、“黄心洋芋”和“白心洋芋”三个不同品种的洋芋。
(3)请根据表中数据计算“白心洋芋”密度值为 kg/m3。比较三次的实验数据可以得到结论： 。
| 次数 | 品种 | 成熟度 | 质量/kg | 体积/cm3 | 密度/(kg/m3) |
| 1 | 小紫芋 | 成熟 | 20 | 18 | 1. 11×103 |
| 2 | 黄心洋芋 | 成熟 | 20 | 18. 3 | 1. 09×103 |
| 3 | 白心洋芋 | 成熟 | 20 | 18. 7 |
|
（1）洋芋的密度与种植地点有关等 （2分）
（2）质量 成熟度 （2分）
（3）1.07×103 洋芋的密度与洋芋的品种有关
解析:略
天天向上一本好卷系列答案
小学生10分钟应用题系列答案（本题满分12分）某品牌的汽车4S店，对最近100位采用分期付款的购车者进行统计，统计结果如右表所示：
| 付款方式 | 分l期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
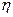表示经销一辆汽车的利润（Ⅰ）求上表中a，b的值
（Ⅱ）若以频率作为概率，求事件A：“购买该品牌汽车的3位顾客中，至多有l位采用3期付款”的概率P（A）
（Ⅲ）求
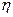的分布列及数学期望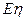
A．洋芋的密度与品种有关；
B．洋芋的密度与质量有关；
C．洋芋的密度与成熟度有关。
(1)请你根据生活经验，再提出一个猜想： 。
(2)为了验证猜想A，需要控制洋芋的 和 ，为此他们从市场上选购了“小紫芋”、“黄心洋芋”和“白心洋芋”三个不同品种的洋芋。
(3)请根据表中数据计算“白心洋芋”密度值为 kg/m3。比较三次的实验数据可以得到结论： 。
| 次数 | 品种 | 成熟度 | 质量/kg | 体积/cm3 | 密度/(kg/m3) |
| 1 | 小紫芋 | 成熟 | 20 | 18 | 1. 11×103 |
| 2 | 黄心洋芋 | 成熟 | 20 | 18. 3 | 1. 09×103 |
| 3 | 白心洋芋 | 成熟 | 20 | 18. 7 | |
（本题6分）某初级中学的同学在学习了“科学探究的方法”和“密度”知识后，产生了探究马铃薯（俗称洋芋）密度的兴趣。他们经过讨论提出如下猜想：
A．洋芋的密度与品种有关；
B．洋芋的密度与质量有关；
C．洋芋的密度与成熟度有关。
(1)请你根据生活经验，再提出一个猜想： 。
(2)为了验证猜想A，需要控制洋芋的 和 ，为此他们从市场上选购了“小紫芋”、“黄心洋芋”和“白心洋芋”三个不同品种的洋芋。
(3)请根据表中数据计算“白心洋芋”密度值为 kg/m3。比较三次的实验数据可以得到结论： 。
| 次数 | 品种 | 成熟度 | 质量/kg | 体积/cm3 | 密度/(kg/m3) |
| 1 | 小紫芋 | 成熟 | 20 | 18 | 1. 11×103 |
| 2 | 黄心洋芋 | 成熟 | 20 | 18. 3 | 1. 09×103 |
| 3 | 白心洋芋 | 成熟 | 20 | 18. 7 | |
（本题6分）某初级中学的同学在学习了“科学探究的方法”和“密度”知识后，产生了探究马铃薯（俗称洋芋）密度的兴趣。他们经过讨论提出如下猜想：
A．洋芋的密度与品种有关；
B．洋芋的密度与质量有关；
C．洋芋的密度与成熟度有关。
(1)请你根据生活经验，再提出一个猜想： 。
(2)为了验证猜想A，需要控制洋芋的 和 ，为此他们从市场上选购了“小紫芋”、“黄心洋芋”和“白心洋芋”三个不同品种的洋芋。
(3)请根据表中数据计算“白心洋芋”密度值为 kg/m3。比较三次的实验数据可以得到结论： 。
|
次数 |
品种 |
成熟度 |
质量/kg |
体积/cm3 |
密度/(kg/m3) |
|
1 |
小紫芋 |
成熟 |
20 |
18 |
1. 11×103 |
|
2 |
黄心洋芋 |
成熟 |
20 |
18. 3 |
1. 09×103 |
|
3 |
白心洋芋 |
成熟 |
20 |
18. 7 |
|