题目内容
 (2013?本溪)如图所示,电源电压保持不变,L是标有“2V 1W”字样的灯泡,电流表A、A1的量程均为0~0.6A,将滑动变阻器滑片P滑至最右端,断开S1,闭合S2,电压表示数为6V,电流表A的示数为0.3A;闭合S1、S2,电流表A1的示数为0.1A.(假设灯丝电阻不变)则下列说法中正确的是( )
(2013?本溪)如图所示,电源电压保持不变,L是标有“2V 1W”字样的灯泡,电流表A、A1的量程均为0~0.6A,将滑动变阻器滑片P滑至最右端,断开S1,闭合S2,电压表示数为6V,电流表A的示数为0.3A;闭合S1、S2,电流表A1的示数为0.1A.(假设灯丝电阻不变)则下列说法中正确的是( )分析:(1)断开S1、闭合S2,电路为滑动变阻器最大阻值的简单电路,电压表的读数就是电源电压,由欧姆定律可求得滑动变阻器的最大阻值;
(2)闭合S1、S2,电阻R0并联在电源上,电流表测该支路的电流,由欧姆定律可求得R0的阻值;
(3)S1断开,S2闭合时电路为滑动变阻器的简单电路,电压表测电源的电压,当S2断开时滑动变阻器与灯泡串联,电压表测滑动变阻器两端的电压,根据并联电路的电压特点可知电压表示数的变化;
(4)断开S1、S2,滑动变阻器与电灯串联,根据P=UI求出灯泡正常发光时的电流,然后结合电流表的量程确定电路的最大电流,此时滑动变阻器接入电路中的电阻最小,根据串联电路的电压特点求出滑动变阻器两端的电压,利用欧姆定律求出滑动变阻器接入电路中的最小阻值.
(2)闭合S1、S2,电阻R0并联在电源上,电流表测该支路的电流,由欧姆定律可求得R0的阻值;
(3)S1断开,S2闭合时电路为滑动变阻器的简单电路,电压表测电源的电压,当S2断开时滑动变阻器与灯泡串联,电压表测滑动变阻器两端的电压,根据并联电路的电压特点可知电压表示数的变化;
(4)断开S1、S2,滑动变阻器与电灯串联,根据P=UI求出灯泡正常发光时的电流,然后结合电流表的量程确定电路的最大电流,此时滑动变阻器接入电路中的电阻最小,根据串联电路的电压特点求出滑动变阻器两端的电压,利用欧姆定律求出滑动变阻器接入电路中的最小阻值.
解答:解:(1)断开S1、闭合S2,电路为滑动变阻器最大阻值的简单电路,电压表测电源的电压即U=6V,
由I=
可得,滑动变阻器的最大阻值:
R滑=
=
=20Ω,故A正确;
(2)闭合S1、S2,电阻R0可以接到电源上,电流表A1的示数即为R0的电流,则
R0=
=
=60Ω,故B正确;
(3)S1断开,S2由闭合到断开时,电压表由测电源的电压变为测滑动变阻器与灯泡串联时滑动变阻器两端的电压,
∵串联电路中总电压等于各分电压之和,
∴电压表的示数变小,故C不正确;
(4)由P=UI可得,灯泡的正常发光时的电流
IL=
=
=0.5A,
∵串联电路中各处的电流相等,且电流表的量程为0~0.6A,
∴电路中的最大电流Imax=0.5A,此时滑动变阻器接入电路中的电阻最小,
滑动变阻器两端的电压:
U滑=U-UL=6V-2V=4V,
滑动变阻器接入电路中的最小值:
R滑=
=
=8Ω,故D选项正确.
故选ABD.
由I=
| U |
| R |
R滑=
| U |
| I |
| 6V |
| 0.3A |
(2)闭合S1、S2,电阻R0可以接到电源上,电流表A1的示数即为R0的电流,则
R0=
| U |
| I0 |
| 6V |
| 0.1A |
(3)S1断开,S2由闭合到断开时,电压表由测电源的电压变为测滑动变阻器与灯泡串联时滑动变阻器两端的电压,
∵串联电路中总电压等于各分电压之和,
∴电压表的示数变小,故C不正确;
(4)由P=UI可得,灯泡的正常发光时的电流
IL=
| PL |
| UL |
| 1W |
| 2V |
∵串联电路中各处的电流相等,且电流表的量程为0~0.6A,
∴电路中的最大电流Imax=0.5A,此时滑动变阻器接入电路中的电阻最小,
滑动变阻器两端的电压:
U滑=U-UL=6V-2V=4V,
滑动变阻器接入电路中的最小值:
R滑=
| U滑 |
| Imax |
| 4V |
| 0.5A |
故选ABD.
点评:本题考查了开关的状态对电路的连接方式的影响和利用欧姆定律、电功率公式的综合计算,仔细判断用电器在开关的不同状态下的连接形式和灵活应用电学中的公式是关键.

练习册系列答案
相关题目
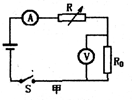 (2013?本溪)如图,是某煤气泄漏检测装置的简化电路,其中电源电压保持不变,R0为定值电阻,R为气体传感器电阻,其阻值随煤气浓度的增大而减小,闭合开关,下列说法中正确的是( )
(2013?本溪)如图,是某煤气泄漏检测装置的简化电路,其中电源电压保持不变,R0为定值电阻,R为气体传感器电阻,其阻值随煤气浓度的增大而减小,闭合开关,下列说法中正确的是( )
 (2013?本溪)如图所示,一条光线垂直射到一个横截面为等腰直角三角形的玻璃砖上,在玻璃砖的平面上安装了一块平面镜.请画出这条光线进入玻璃砖射到平面镜上,经反射后射回空气中的光路图.
(2013?本溪)如图所示,一条光线垂直射到一个横截面为等腰直角三角形的玻璃砖上,在玻璃砖的平面上安装了一块平面镜.请画出这条光线进入玻璃砖射到平面镜上,经反射后射回空气中的光路图. (2013?本溪)如图所示,为了学生的安全我省购置了一批“大鼻子”校车,校车满员时人和车的总质量为1.0×106kg.车轮的总着地面积为0.25m2.校车以36km/h的速度在平直公路上匀速直线行驶10min,所受阻力是总重力的0.01倍.请计算:(g=10N/kg)
(2013?本溪)如图所示,为了学生的安全我省购置了一批“大鼻子”校车,校车满员时人和车的总质量为1.0×106kg.车轮的总着地面积为0.25m2.校车以36km/h的速度在平直公路上匀速直线行驶10min,所受阻力是总重力的0.01倍.请计算:(g=10N/kg)