题目内容
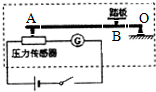 (2010?宝应县模拟)有一种测量人体重的电子秤,其原理图如图中的虚线所示,它主要由三部分构成:踏板和压力杠杆ABO、压力传感器R(一个阻值可随压力大小而变化的电阻器),显示体重的仪表G(其实质是电流表),其中AO:BO=5:1.已知压力传感器的电阻与其所受压力的关系如下表所示:
(2010?宝应县模拟)有一种测量人体重的电子秤,其原理图如图中的虚线所示,它主要由三部分构成:踏板和压力杠杆ABO、压力传感器R(一个阻值可随压力大小而变化的电阻器),显示体重的仪表G(其实质是电流表),其中AO:BO=5:1.已知压力传感器的电阻与其所受压力的关系如下表所示:| 压力F/N | 0 | 50 | 100 | 150 | 200 | 250 | 300 | … |
| 电阻R/SKIPIF 1<0 | 300 | 270 | 240 | 210 | 180 | 150 | 120 | … |
则:(1)利用表中数据归纳出电阻R随压力F变化的函数关系式:
R=300-0.6F
R=300-0.6F
;(2)该秤零刻度线(即踏板空载时的刻度线)应标在电流表刻度盘
15.6
15.6
毫安处;(3)如果某人站在踏板上,电流表刻度盘示数为20mA,这个人的体重是
550N
550N
.分析:(1)观察表格中的数据可知,压力每增大50N,压力传感器的电阻减小30Ω,据此可归纳出R随压力F变化的函数关系式;
(2)踏板空载时,通过表中信息可以得出电阻大小,利用欧姆定律可以求电流;
(3)根据电压与电流可求出此时压力传感器的电阻值,再依据表中的变化规律可求出此时作用在A点的压力的大小,最后根据杠杆的平衡条件得出作用在B点的人的体重;
(2)踏板空载时,通过表中信息可以得出电阻大小,利用欧姆定律可以求电流;
(3)根据电压与电流可求出此时压力传感器的电阻值,再依据表中的变化规律可求出此时作用在A点的压力的大小,最后根据杠杆的平衡条件得出作用在B点的人的体重;
解答:解:(1)分析数据可知,当F每增大50N时,电阻R减小30Ω,因为电阻的最大值为300Ω,所以归纳得电阻R随压力F变化的函数关系式为:R=300-0.6F;
(2)读表格可知,当压力为0时,压力传感器的电阻为300Ω,则电路中的电流I1=
=
=0.0156A=15.6mA;
(3)当电流为20mA时,压力传感器的电阻为R2=
=
=234Ω,
根据R随压力F的变化函数关系R=300-0.6F得,F2=(300Ω-234Ω)÷0.6=110N,
设人的体重为G,根据杠杆的平衡条件得,F2?AO=G?BO
解得,G=
=110N×
=550N
故答案为:(1)R=300-0.6F; (2)15.6; (3)550N.
(2)读表格可知,当压力为0时,压力传感器的电阻为300Ω,则电路中的电流I1=
| U |
| R1 |
| 4.68V |
| 300Ω |
(3)当电流为20mA时,压力传感器的电阻为R2=
| U |
| I2 |
| 4.68V |
| 0.02A |
根据R随压力F的变化函数关系R=300-0.6F得,F2=(300Ω-234Ω)÷0.6=110N,
设人的体重为G,根据杠杆的平衡条件得,F2?AO=G?BO
解得,G=
| F2?AO |
| BO |
| 5 |
| 1 |
故答案为:(1)R=300-0.6F; (2)15.6; (3)550N.
点评:理解这一装置的工作原理,是解决此题的前提,此题中主要考查了实验数据的分析、欧姆定律的应用、杠杆平衡条件的应用等,具有一定的综合性,也对我们分析题意的能力提出了较高的要求.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
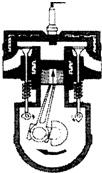 (2010?宝应县模拟)一台单缸四冲程汽油机的飞轮转速是1200r/min,则汽油机每秒完成
(2010?宝应县模拟)一台单缸四冲程汽油机的飞轮转速是1200r/min,则汽油机每秒完成 (2010?宝应县模拟)做物理实验要遵循实事求是的原则.如图所示,小明同学在“研究定滑轮和动滑轮特点”的实验中,完成了如下所示的实验,并记录了数据(如下表).
(2010?宝应县模拟)做物理实验要遵循实事求是的原则.如图所示,小明同学在“研究定滑轮和动滑轮特点”的实验中,完成了如下所示的实验,并记录了数据(如下表).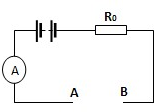 (2010?宝应县模拟)育才中学物理课外兴趣小组的同学在课外活动中探究一段电路的电功率和这段电路电阻的关系.实际的电路如图所示,电源电压保持不变,R0=4Ω,为定值电阻.他们在A、B间先后串联不同个数的相同电阻R,并分别测量出电路中电流I和A、B段的电功率PAB,测得的数据如下表所示(表中省略号部分不用填写)
(2010?宝应县模拟)育才中学物理课外兴趣小组的同学在课外活动中探究一段电路的电功率和这段电路电阻的关系.实际的电路如图所示,电源电压保持不变,R0=4Ω,为定值电阻.他们在A、B间先后串联不同个数的相同电阻R,并分别测量出电路中电流I和A、B段的电功率PAB,测得的数据如下表所示(表中省略号部分不用填写)