题目内容
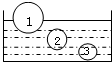 (2013?和平区一模)三个实心球静止在某种液体的位置如图,球1有一半体积浸在液面下,球2和球3的密度ρ2:ρ3=2:3,三球半径r1:r 2:r3=3:2:1.球的体积公式为V=
(2013?和平区一模)三个实心球静止在某种液体的位置如图,球1有一半体积浸在液面下,球2和球3的密度ρ2:ρ3=2:3,三球半径r1:r 2:r3=3:2:1.球的体积公式为V=| 4m3 |
| 3 |
分析:①利用体积公式计算出体积比,然后利用密度公式计算出甲乙丙的质量比即三球所受重力比;
利用三个球的密度关系和半径关系求出其质量关系,进而可以求得三者的重力关系.
根据甲球、乙球、丙球的体积关系以及所在液体的密度关系利用阿基米德原理可以求得三者所受的浮力大小关系.
利用三个球的密度关系和半径关系求出其质量关系,进而可以求得三者的重力关系.
根据甲球、乙球、丙球的体积关系以及所在液体的密度关系利用阿基米德原理可以求得三者所受的浮力大小关系.
解答:解:(1)1球漂浮,V1排=
=
×
πr3=π×(r1)3=
×
π(3r)3=18πr33;
2球悬浮,V2排=
πr3=
π(2r)3=
πr33;
3球下沉,此时的V3排=
πr3;
故由F浮=ρgV排可知,三球所受浮力之比为:F1:F2:F3=27:16:2,B错误,A正确;
(2)球1有一半体积浸在液面下,即漂浮,即F浮=ρ液g
V物=G物=ρ物V物g,所以ρ物=
ρ液;
因2球悬浮,所以ρ乙=ρ液,
所以ρ1:ρ2:ρ3=1:2:3,
由G=mg=ρ物gV,可知:
G1:G2:G3=ρ1V1:ρ2V2:ρ3V3=ρ1×36πr33:ρ2×
πr33:ρ3×
πr33=27:16:3,C正确,D错误;
故选AC.
| V甲 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
2球悬浮,V2排=
| 4 |
| 3 |
| 4 |
| 3 |
| 32 |
| 3 |
3球下沉,此时的V3排=
| 4 |
| 3 |
故由F浮=ρgV排可知,三球所受浮力之比为:F1:F2:F3=27:16:2,B错误,A正确;
(2)球1有一半体积浸在液面下,即漂浮,即F浮=ρ液g
| 1 |
| 2 |
| 1 |
| 2 |
因2球悬浮,所以ρ乙=ρ液,
所以ρ1:ρ2:ρ3=1:2:3,
由G=mg=ρ物gV,可知:
G1:G2:G3=ρ1V1:ρ2V2:ρ3V3=ρ1×36πr33:ρ2×
| 32 |
| 3 |
| 4 |
| 3 |
故选AC.
点评:本题涉及知识点多,易出错;涉及浮力知识,要灵活利用密度公式,重力公式,漂浮、悬浮的条件等公式计算.

练习册系列答案
相关题目
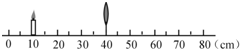 (2013?和平区一模)如图是用来研究凸透镜成像规律的实验装置示意图(屏未画出),当蜡烛和透镜放在图示位置时,通过移动光屏,可以在光屏上得到与物体等大的像.( )
(2013?和平区一模)如图是用来研究凸透镜成像规律的实验装置示意图(屏未画出),当蜡烛和透镜放在图示位置时,通过移动光屏,可以在光屏上得到与物体等大的像.( )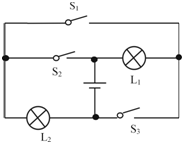 (2013?和平区一模)如图所示电路,只闭合开关
(2013?和平区一模)如图所示电路,只闭合开关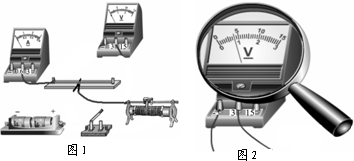 (2013?和平区一模)探究导体的电阻跟导体长度的关系的电路如图1所示,通过移动导线夹可改变接入电路中电阻丝的长度.
(2013?和平区一模)探究导体的电阻跟导体长度的关系的电路如图1所示,通过移动导线夹可改变接入电路中电阻丝的长度.