题目内容
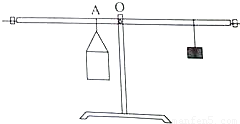
如图装置为某学生在科技创新大赛时发明的可以直接测量液体密度的“密度天平”.其制作过程和原理如下:选择一根长1米的杠杆,调节两边螺母使杠杆在水平位置平衡.在左侧离中点10厘米的A位置用细线固定一个质量为150克、容积为80毫升的容器.右侧用细线悬挂一质量为50克的钩码(细线的质量忽略不计).测量时往容器中加满待测液体,移动钩码使杠杆在水平位置平衡,在钩码悬挂位置直接读出液体的密度.(1)该“密度天平”的“零刻度”应标在右端离支点O______厘米处.
(2)该“密度天平”的量程为多大?
(3)若将钩码的质量适当增大,该“密度天平”的量程将______(选填“增大”“减小”或“不变”).
【答案】分析:(1)在容器中未倒入液体时,直接将相关数据带入杠杆的平衡条件公式F1L1=F2L2中,即可求出钩码所在的位置,这就是该“密度天平”的“零刻度”;
(2)钩码移至最右端时,该“密度天平”达到了大量程,同样根据杠杆的平衡条件,带入相关的数据,即可进行求解;
(3)钩码的质量适当增大,说明杠杆一侧的力增大,在力臂关系相同的情况下,另一侧的力也会增大,即该“密度天平”的量程将增大.
解答:解:(1)根据杠杆的平衡条件公式F1L1=F2L2得,150g×10cm=50g×L2,
解得,L2=30cm.
(2)根据题意钩码移动至最右端,该“密度天平”达到最大量程,设OA为L1′,O点距最右端的距离为L2′,容器的质量为m1,钩码的质量为m2,容器中加满液体的质量为m,
由F1L1=F2L2得,(m1+m)gL1′=m2gL2,
已知:m1=150g,m2=50g,L1=10cm,L2=50cm,
代入上式解得,m=100g,
ρ=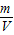 =
=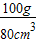 =1.25g/cm3.
=1.25g/cm3.
(3)当钩码的质量适当增大时,说明杠杆一侧的力增大,在力臂关系相同的情况下,另一侧的力也会增大,即该“密度天平”的量程将增大.
故答案为:(1)30;
(2)该“密度天平”的量程为0~1.25g/cm3.
(3)增大.
点评:通过杠杆的平衡条件,来间接地测量液体的密度,题目考查的角度比较新颖,能熟练运用杠杆的平衡条件进行分析,并能将相关数据对号入座,最终转换为密度的测量是本题的关键.
(2)钩码移至最右端时,该“密度天平”达到了大量程,同样根据杠杆的平衡条件,带入相关的数据,即可进行求解;
(3)钩码的质量适当增大,说明杠杆一侧的力增大,在力臂关系相同的情况下,另一侧的力也会增大,即该“密度天平”的量程将增大.
解答:解:(1)根据杠杆的平衡条件公式F1L1=F2L2得,150g×10cm=50g×L2,
解得,L2=30cm.
(2)根据题意钩码移动至最右端,该“密度天平”达到最大量程,设OA为L1′,O点距最右端的距离为L2′,容器的质量为m1,钩码的质量为m2,容器中加满液体的质量为m,
由F1L1=F2L2得,(m1+m)gL1′=m2gL2,
已知:m1=150g,m2=50g,L1=10cm,L2=50cm,
代入上式解得,m=100g,
ρ=
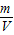 =
=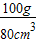 =1.25g/cm3.
=1.25g/cm3.(3)当钩码的质量适当增大时,说明杠杆一侧的力增大,在力臂关系相同的情况下,另一侧的力也会增大,即该“密度天平”的量程将增大.
故答案为:(1)30;
(2)该“密度天平”的量程为0~1.25g/cm3.
(3)增大.
点评:通过杠杆的平衡条件,来间接地测量液体的密度,题目考查的角度比较新颖,能熟练运用杠杆的平衡条件进行分析,并能将相关数据对号入座,最终转换为密度的测量是本题的关键.

练习册系列答案
相关题目
 在科学实验中要规范操作,了解仪器性能,保障安全.
在科学实验中要规范操作,了解仪器性能,保障安全.
(1)小科学习了弹簧秤的刻度原理后,十分兴奋,决定自制一把弹簧秤.他找来了弹簧A及其它器材,利用如图实验装置,研究了弹簧的长度跟外力的变化关系,记录相应数据如下:
小科在制作弹簧秤时仔细分析数据后得出弹簧秤的量程为________.
| 钩码重/N | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
| 指针位置/cm | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 26.8 | 27.5 |

 (3)为了定性研究液体压强的特点,老师要学生准备了如下器材:透明塑料饮料瓶、剪刀、细线、几个大小不同的气球.为了验证液体内部的压强随深度的增加而增大这一结论,小明用剪刀剪去饮料瓶底,在瓶盖上扎一小孔,然后用细线系住吹起的小气球,通过瓶盖上的小孔将气球拉入瓶内,将瓶倒置,用手堵住瓶盖上的小孔,再向瓶内注水,如图所示.为了达到实验目的,小明接下来应通过________调整气球在水中的深度,同时观察气球的________.
(3)为了定性研究液体压强的特点,老师要学生准备了如下器材:透明塑料饮料瓶、剪刀、细线、几个大小不同的气球.为了验证液体内部的压强随深度的增加而增大这一结论,小明用剪刀剪去饮料瓶底,在瓶盖上扎一小孔,然后用细线系住吹起的小气球,通过瓶盖上的小孔将气球拉入瓶内,将瓶倒置,用手堵住瓶盖上的小孔,再向瓶内注水,如图所示.为了达到实验目的,小明接下来应通过________调整气球在水中的深度,同时观察气球的________.
在科学实验中要规范操作,了解仪器性能,保障安全.
(1)小科学习了弹簧秤的刻度原理后,十分兴奋,决定自制一把弹簧秤.他找来了弹簧A及其它器材,利用如图实验装置,研究了弹簧的长度跟外力的变化关系,记录相应数据如下:
小科在制作弹簧秤时仔细分析数据后得出弹簧秤的量程为______.
(2)如图所示,某同学将自己戴的近视眼镜放在蜡烛与凸透镜之间,在光屏上得到一个清晰的像.在下列表示视力矫正的光路图中,与上述实验情形一致的是______.

(3)为了定性研究液体压强的特点,老师要学生准备了如下器材:透明塑料饮料瓶、剪刀、细线、几个大小不同的气球.为了验证液体内部的压强随深度的增加而增大这一结论,小明用剪刀剪去饮料瓶底,在瓶盖上扎一小孔,然后用细线系住吹起的小气球,通过瓶盖上的小孔将气球拉入瓶内,将瓶倒置,用手堵住瓶盖上的小孔,再向瓶内注水,如图所示.为了达到实验目的,小明接下来应通过______调整气球在水中的深度,同时观察气球的______.


(1)小科学习了弹簧秤的刻度原理后,十分兴奋,决定自制一把弹簧秤.他找来了弹簧A及其它器材,利用如图实验装置,研究了弹簧的长度跟外力的变化关系,记录相应数据如下:
小科在制作弹簧秤时仔细分析数据后得出弹簧秤的量程为______.
| 钩码重/N | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | |
| 指针位置/cm | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 26.8 | 27.5 |

(3)为了定性研究液体压强的特点,老师要学生准备了如下器材:透明塑料饮料瓶、剪刀、细线、几个大小不同的气球.为了验证液体内部的压强随深度的增加而增大这一结论,小明用剪刀剪去饮料瓶底,在瓶盖上扎一小孔,然后用细线系住吹起的小气球,通过瓶盖上的小孔将气球拉入瓶内,将瓶倒置,用手堵住瓶盖上的小孔,再向瓶内注水,如图所示.为了达到实验目的,小明接下来应通过______调整气球在水中的深度,同时观察气球的______.


 在科学实验中要规范操作,了解仪器性能,保障安全.
在科学实验中要规范操作,了解仪器性能,保障安全.
 (3)为了定性研究液体压强的特点,老师要学生准备了如下器材:透明塑料饮料瓶、剪刀、细线、几个大小不同的气球.为了验证液体内部的压强随深度的增加而增大这一结论,小明用剪刀剪去饮料瓶底,在瓶盖上扎一小孔,然后用细线系住吹起的小气球,通过瓶盖上的小孔将气球拉入瓶内,将瓶倒置,用手堵住瓶盖上的小孔,再向瓶内注水,如图所示.为了达到实验目的,小明接下来应通过
(3)为了定性研究液体压强的特点,老师要学生准备了如下器材:透明塑料饮料瓶、剪刀、细线、几个大小不同的气球.为了验证液体内部的压强随深度的增加而增大这一结论,小明用剪刀剪去饮料瓶底,在瓶盖上扎一小孔,然后用细线系住吹起的小气球,通过瓶盖上的小孔将气球拉入瓶内,将瓶倒置,用手堵住瓶盖上的小孔,再向瓶内注水,如图所示.为了达到实验目的,小明接下来应通过