题目内容
一底面积是100cm2的柱形容器内盛有适量的水,现将含有石块的冰块投入容器内的水中,恰好悬浮,此时水位上升了6cm。当水中冰块全部熔化后,相比熔化前水对容器底部的压强改变了55.28Pa。则石块的密度为 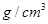 。
。
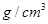 。
。2.17×103
试题分析:含有石块的冰块悬浮时,水位上升了△h=6cm=0.06m,
冰块和石块的总体积:
V总=S×△h=100×10﹣4m2×0.06m=6×10﹣4m3,
(m石+m冰)g=F浮=G排=ρ水gS×△h=1000kg/m3×10N/kg×0.01m2×0.06m=6N,
∴石块和冰的总质量:
(m石+m冰)=
 =0.6kg,
=0.6kg,冰熔化后,水位下降的高度:
h降=
 =5.528×10﹣3m,
=5.528×10﹣3m,冰熔化成水质量m不变,
∵
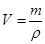
∴,
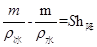
冰的质量:
m=S×h降×
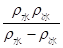 =100×10﹣4m2×5.528×10﹣3m×
=100×10﹣4m2×5.528×10﹣3m×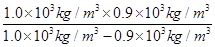 =0.49752kg,
=0.49752kg,石块质量:
m石=0.6kg﹣0.49752kg=0.10248kg,
石块体积:
V石=V总﹣V冰=V总﹣
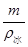 =6×10﹣4m3﹣
=6×10﹣4m3﹣ =4.72×10﹣5m3,
=4.72×10﹣5m3,石块的密度:
ρ石=
 =
= =2.17×103kg/m3.
=2.17×103kg/m3.点评:冰块悬浮时水位上升了6cm,据此求出冰块和石块的总体积,根据悬浮条件求冰块和石块的总重、总质量;
根据液体压强公式求冰溶化后水位下降的高度,因为冰熔化后质量不变,冰的体积减去熔化成水的体积等于减小的体积,根据此等式求出冰的质量,从而求出石块的质量;
根据求得的冰的质量计算出冰的体积,又知道总体积,两者之差即为石块的体积,根据公式
 求出石块的密度.
求出石块的密度.
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目




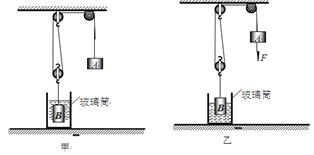
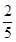 的体积露出水面且静止,此时滑轮组提升重物B的机械效率为80%,水对容器底的压强为2100 Pa。 g取10N/kg,悬挂物体的细绳的质量以及绳与轮间的摩擦忽略不计,物体A的密度是 kg/m3。
的体积露出水面且静止,此时滑轮组提升重物B的机械效率为80%,水对容器底的压强为2100 Pa。 g取10N/kg,悬挂物体的细绳的质量以及绳与轮间的摩擦忽略不计,物体A的密度是 kg/m3。