题目内容
 (2011?咸宁)如图1所示将边长为10cm的密度均匀的正方体木块平放在圆柱形容器的底部,圆柱形容器的横截面积为300cm2,此时正方体木块对圆柱形容器的底部的压强是800N/m2.现缓慢地往容器中注水,当容器中的水面升至一定高度时,木块对容器底面的压力恰好为零,如图2所示.已知g=10N/kg,ρ水=1.0×103kg/m3.求:
(2011?咸宁)如图1所示将边长为10cm的密度均匀的正方体木块平放在圆柱形容器的底部,圆柱形容器的横截面积为300cm2,此时正方体木块对圆柱形容器的底部的压强是800N/m2.现缓慢地往容器中注水,当容器中的水面升至一定高度时,木块对容器底面的压力恰好为零,如图2所示.已知g=10N/kg,ρ水=1.0×103kg/m3.求:(1)木块的密度ρ木是多少千克每立方米??
(2)水面上升的高度h是多少厘米?
(3)注入水的质量m是多少千克?
分析:(1)设正方体木块的边长为L,圆柱形容器的横截面积为S,根据此时正方体木块对圆柱形容器的底部的压强是800N/m2,可求出正方体木块对圆柱形容器的底部的压力,此时压力即为其重力,再根据G=mg可得出其质量,再利用ρ=
可求得木块的密度.
(2)由于木块此时对容器底的压力为零,所以,木块此时受到的浮力等于木块的重力:即G木=F浮=ρ水gV排可求得水面上升的高度h.
(3)由题意可知,注入水的体积为圆柱形容器的横截面积减去正方体木块的底面积再乘以水面上升的高度h,再利用密度公式变形m=ρV即可求出注入水的质量.
| m |
| V |
(2)由于木块此时对容器底的压力为零,所以,木块此时受到的浮力等于木块的重力:即G木=F浮=ρ水gV排可求得水面上升的高度h.
(3)由题意可知,注入水的体积为圆柱形容器的横截面积减去正方体木块的底面积再乘以水面上升的高度h,再利用密度公式变形m=ρV即可求出注入水的质量.
解答:解:(1)设正方体木块的边长为L,因此时正方体木块对圆柱形容器的底部的压强是800N/m2.圆柱形容器的横截面积为S.
所以由P=
,可得F=PL2=800N/m2×100×10-4m2=8N,
G=F=8N,m木=
=
=0.8kg.
ρ木=
=
=0.8×103 kg/m3.
答:木块的密度ρ木是0.8×103 kg/m3.
(2)由于木块此时对容器底的压力为零,所以,木块此时受到的浮力等于木块的重力:即G木=F浮=ρ水gV排,
即由G木=ρ水ghL2得8N=1.0×103 kg/m3×10N/kg×100×10-4m2h,
解得h=0.08m=8cm.
答:水面上升的高度h是8cm.
(3)V水=(S-L2)h=(300cm2-100cm2)×8cm=1600cm2=1.6×10-3m3,
m=ρ水V水=1.0×103kg/m3×1.6×10-3m3=1.6kg.
答:注入水的质量m是1.6kg.
所以由P=
| F |
| L2 |
G=F=8N,m木=
| G |
| g |
| 8N |
| 10N/kg |
ρ木=
| m木 |
| L3 |
| 0.8kg |
| 10-3m3 |
答:木块的密度ρ木是0.8×103 kg/m3.
(2)由于木块此时对容器底的压力为零,所以,木块此时受到的浮力等于木块的重力:即G木=F浮=ρ水gV排,
即由G木=ρ水ghL2得8N=1.0×103 kg/m3×10N/kg×100×10-4m2h,
解得h=0.08m=8cm.
答:水面上升的高度h是8cm.
(3)V水=(S-L2)h=(300cm2-100cm2)×8cm=1600cm2=1.6×10-3m3,
m=ρ水V水=1.0×103kg/m3×1.6×10-3m3=1.6kg.
答:注入水的质量m是1.6kg.
点评:解决较复杂的物理题,一定要搞清楚各个量之间的关系.在此题中,可以通过画图的方法,把S木、S底、S水三者之间的关系搞清楚.
题目中告诉的:木块对容器底面的压力恰好为零这句话是求解木块的重力关键.
题目中告诉的:木块对容器底面的压力恰好为零这句话是求解木块的重力关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

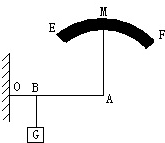 (2011?咸宁)如图所示,杠杆OA的B点挂着重物G,A端用细绳挂在圆弧EF上,此时OA恰成水平,且A点与圆弧形架EF的圆心重合.当绳AM的M端从E点缓慢滑到F点的过程中,绳对A点拉力的大小将( )
(2011?咸宁)如图所示,杠杆OA的B点挂着重物G,A端用细绳挂在圆弧EF上,此时OA恰成水平,且A点与圆弧形架EF的圆心重合.当绳AM的M端从E点缓慢滑到F点的过程中,绳对A点拉力的大小将( ) (2011?咸宁)如图是速滑运动员在赛道上奋勇拼搏的镜头.滑冰鞋的冰刀与冰面的接触面积很小是为了增大运动员对冰面的
(2011?咸宁)如图是速滑运动员在赛道上奋勇拼搏的镜头.滑冰鞋的冰刀与冰面的接触面积很小是为了增大运动员对冰面的 (2011?咸宁)如图所示,为了测量人骑自行车的功率,某活动小组进行了如下实验:在离出发线5m、10m、20m、30m、…70m的地方分别划上8条计时线,每条计时线附近站几个学生,手持秒表.听到发令员的信号后,受测者全力骑车由出发线启动,同时全体学生都开始计时.自行车每到达一条计时线,站在该计时线上的几个学生就停止计时,记下自行车从出发线到该条计时线的时间.实验数据记录如下:
(2011?咸宁)如图所示,为了测量人骑自行车的功率,某活动小组进行了如下实验:在离出发线5m、10m、20m、30m、…70m的地方分别划上8条计时线,每条计时线附近站几个学生,手持秒表.听到发令员的信号后,受测者全力骑车由出发线启动,同时全体学生都开始计时.自行车每到达一条计时线,站在该计时线上的几个学生就停止计时,记下自行车从出发线到该条计时线的时间.实验数据记录如下: