Question

【题目】如图所示，一根质量不计的轻棒长度为d，质量为m的物块A用细绳挂于其中点，轻棒可绕转轴O转动转轴处摩擦不计)。用最小的拉力F缓慢将轻棒从竖直位置拉动到与竖直方向夹角为θ=60°的位置。

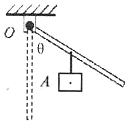
(1)在如图中画出此时的最小拉力F和阻力臂L2________________

(2)在从竖直位置拉向水平位置的过程中，随拉开角度的增加，请推导出拉力F的大小与角度θ的关系式 ________。

(3)从竖直位置拉动到与竖直方向夹角为θ=60°的位置时共用时间t，则拉力F做功功率的表达式是____________________。

(4)拉力F的功率并不是始终这么大，此功率的表达式是表示拉力F做功的__________。

Answer 1

【答案】 0.5mgsinθ 0.25mgd/t 平均快慢程度

【解析】根据力臂的概念：从支点向力的作用线作垂线即力臂；根据杠杆的平衡条件可知力臂最大时力最小，从图上可以看出力与杠杆垂直是力最小，作图如下：

（2）Gdsin=Fd ,F==Gsin=mgsin；

（3）W=Gh=mgdmgd,

P===

(4)拉力F的功率并不是始终这么大，此功率的表达式是表示拉力F做功的平均快慢程度