题目内容
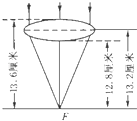
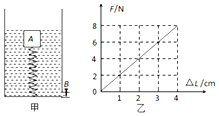
【题目】如图甲所示,在容器底部固定一轻质弹簧,弹簧上端连有一边长为0.1m的正方体物块A,容器中水的深度为40cm时,物块A刚好完全浸没在水中。容器侧面的底部有一个由阀门B控制的出水口,打开阀门B,使水缓慢流出,当物块A有五分之二的体积露出水面时,弹簧恰好处于自然伸长状态(即恢复原长没有发生形变),当物块A刚好全部露出水面时关闭阀门B.弹簧受到的弹力F和弹簧形变大小△L(伸长或缩短的量)成正比,如图乙所示。(g取10N/kg,ρ水=1.0×103kg/m3,不计弹簧所受浮力,物块A不吸水)。求:
(1)物块A的密度;
(2)弹簧的原长;
(3)物块A刚好全部露出水面时水对容器底部的压强。
【答案】(1)0.6×103kg/m3;(2)28cm;(3)2500Pa。
【解析】(1)根据题意知道,当物块A有五分之二的体积露出水面时,弹簧恰好处于自然伸长状态,此时物块A恰好漂浮,又因为物体漂浮时受到的浮力和自身的重力相等,所以,由F浮=ρgV排和G=mg=ρVg知道,ρ水g(1-2/5)V=ρVg,则物块A的密度是:ρ=3ρ水/ 5 =3/5×1.0×103 kg/m3 =0.6×103 kg/m3;
(2)物块A的体积是:V=LA 3 =(0.1m)3 =10-3 m3 ,
由ρ=m/V可得,物块A的质量是:m=ρV=0.6×103 kg/m3 ×10-3 m3 =0.6kg,
当物块A刚好完全浸没在水中时,受到的浮力是:F浮=ρ水gV=1.0×103 kg/m3 ×10N/kg×10-3 m3 =10N,
又因为物体A在竖直向下的重力和弹簧的拉力、竖直上升的浮力作用下处于平衡状态,
所以,弹簧的弹力是是:F=F浮-G=F浮-mg=10N-0.6kg×10N/kg=4N,
由图乙可知道,此时弹簧的伸长量是:△L=2cm时,所以弹簧的原长是L=h-LA -△L=40cm-10cm-2cm=28cm;
(3)物块A刚好全部露出水面时,弹簧的弹力和物体A的重力相等,由图乙知道,弹簧的压缩量是:△L′=3cm,
则容器内水深度的变化量是:h′=h-LA -△L-△L′=40cm-10cm-2cm-3cm=25cm=0.25m,
水对容器底部的压强:p水=ρ水gh′=1.0×103 kg/m3 ×10N/kg×0.25m=2500Pa。