题目内容
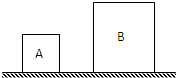 (2012?嘉定区二模)如图所示,实心均匀正方体A、B放置在水平地面上,它们的重均为980牛,A的边长为0.25米,B的边长为0.4米.
(2012?嘉定区二模)如图所示,实心均匀正方体A、B放置在水平地面上,它们的重均为980牛,A的边长为0.25米,B的边长为0.4米.①求正方体A的密度ρA.
②求正方体B对水平地面的压强pB.
③若在正方体A、B上沿水平方向分别截去相同的体积△V后,A、B剩余部分对水平地面的压强pA′和pB′,请通过计算比较它们的大小关系及其对应的△V的取值范围.
分析:(1)知道A的重力,可求出其质量,根据边长求出其的体积,利用密度公式求物体A的密度;
(2)由于物体是静止在水平面上,此时物体对地面的压力F=G,则压强可利用P=
求得;
(3)在正方体A、B上沿水平方向分别截去相同的体积V后,受力面积不变,求出剩余部分对地面的压力、压强;根据剩余部分对地面的压强相等,列出方程求V的大小;进而得出它们对水平地面的压强大小关系及其对应的V的取值范围
(2)由于物体是静止在水平面上,此时物体对地面的压力F=G,则压强可利用P=
| F |
| S |
(3)在正方体A、B上沿水平方向分别截去相同的体积V后,受力面积不变,求出剩余部分对地面的压力、压强;根据剩余部分对地面的压强相等,列出方程求V的大小;进而得出它们对水平地面的压强大小关系及其对应的V的取值范围
解答:解:(1)
ρA=
=
=
=6.4×103千克/米3
(ρB=
=
=1.5625×103千克/米3)
答:正方体A的密度为6.4×103千克/米3
(2)PB=
=
=980牛/(0.4米)2=6.125×103帕.
答:正方体B对水平地面的压强为6.125×103帕.
(3)在正方体A、B上沿水平方向分别截去相同的体积V后,受力面积不变,
∵当PA′=PB′
=
∴
=
=(
)2=
∴当△V=0.010525米3时,pA′=pB′
当0<△V<0.010525米3时,pA′>pB′
当0.015625米3>△V>0.010525米3时,pA′<pB′
ρA=
| mA |
| VA |
| GA |
| VAg |
| 980牛 |
| (0.25米)3×9.8牛/千克 |
(ρB=
| mB |
| VB |
| GB |
| VBg |
答:正方体A的密度为6.4×103千克/米3
(2)PB=
| FB |
| SB |
| GB |
| SB |
答:正方体B对水平地面的压强为6.125×103帕.
(3)在正方体A、B上沿水平方向分别截去相同的体积V后,受力面积不变,
∵当PA′=PB′
| GA-ρA△Vg |
| SA |
| GB-ρB△Vg |
| SB |
∴
| GA-ρA△Vg |
| GB-ρB△Vg |
| SA |
| SB |
| aA |
| aB |
| 25 |
| 64 |
∴当△V=0.010525米3时,pA′=pB′
当0<△V<0.010525米3时,pA′>pB′
当0.015625米3>△V>0.010525米3时,pA′<pB′
点评:本题考查了压强的计算、密度的计算,在解题时要记住相关公式,灵活运用密度公式解决比值问题,最后对压强PA′和PB′的大小关系展开讨论.确定两种情况下的地面受力大小和受力面积是本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 (2012?嘉定区二模)如图所示,吹笛子时用手指按住不同的笛孔,这主要是用来改变声音的( )
(2012?嘉定区二模)如图所示,吹笛子时用手指按住不同的笛孔,这主要是用来改变声音的( )