��Ŀ����
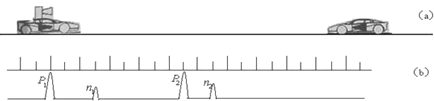
����Ŀ����ͼ��a����ʾ��ͣ�ڹ�·�ԵĹ���Ѳ�߳����ó��������Լ��٣�Ѳ�߳��ϲ����Ƿ��������ճ����������źţ����ݷ����ͽ��յ����źż��ʱ�����ܲ�����٣���ͼ��b���У�P1��P2�Dz������Ⱥ��ij������źţ�n1 n2�ֱ��Dz����Ǽ���P1��P2���������źţ������������ɨ�裬P1��P2֮���ʱ����Ϊ0.9�룬�������ڿ����д������ٶ�Ϊ340��/�룬��ij���Ϊ���٣�
���𰸡�20m/s
��������
�����������1���������֪��P1��P2��ʱ����Ϊ0.9s������ͼ����ʾP1��P2�ļ���Ŀ̶�ֵ���Լ�P1��n1��P2��n2֮�����Ŀ̶�ֵ���������P1��n1��P2��n2���ʱ�䣬���������ɷ�������������Ҫ��ʱ�䣻�Ӷ��������������ǰ�����δӲ������������õ�ʱ�䣬������٣������������ǰ������������������֮��ľ��룻�����������Ų����Ƿ����˶�����������֮��ľ����ڼ�С������ǰ�����ε�������֮��ľ���֮�Ϊ����ǰ����·�̣�
��2���������γ�����������ʱ����Ϊ0.9s�������˶���ʱ��Ϊ�ӵ�һ���볬����������ʼ�����ڶ����볬��������������������ʱ�䣬���������˶���ʱ�䣮
��3�����������˶��ľ����ʱ�䣬��������������˶��ٶȣ�
�⣺��1��P1��P2�ļ���Ŀ̶�ֵΪ4.5����ʱ�䳤Ϊ0.9s��P1��n1֮�����Ŀ̶�ֵΪ1.5�������Զ�Ӧ��ʱ��Ϊ0.3s�������ǵ�һ�η���������ʱ��������0.15s�����������������źŴ����������ز����ǣ�Ҳ��ʻ��0.15s��ʱ�䣻
P2��n2֮�����Ŀ̶�ֵ1�������Զ�Ӧ��������֮���Ӧ��ʱ��Ϊ0.2s�������ǵڶ��η���������ʱ��������0.1s�����������������źŴ����������ز����ǣ�Ҳ��ʻ��0.1s��ʱ�䣻
�����ǵ�һ�η������źŴ����������ص�������ʱ������������ǣ�
s1=v��t1=340m/s��0.15s=51m��
�ڶ��η������źŴ����������ص�������ʱ������������ǣ�
s2=v��t2=340m/s��0.1s=34m��
����������������ź������Ĺ����У���ʻ�ˣ�s��=s1��s2=51m��34m=17m��
��2����17m�����ˣ�t��=��t��![]() +
+![]() =0.9s��0.15s+0.1s=0.85s��
=0.9s��0.15s+0.1s=0.85s��
��3�����������ij�����v��=![]() =
=![]() =20m/s��
=20m/s��
�𣺱����������ٶ�Ϊ20m/s��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�



