题目内容
 (2012?青岛模拟)问题解决:
(2012?青岛模拟)问题解决:小明同学想测出某种液体的密度,他手边只有一个两端开口的玻璃管、橡皮膜、刻度尺、大烧杯和足量的水.要求:
(1)推导出这种液体密度的数学表达式;
(2)请简要写出他的测量步骤.(配图说明,图画在方框内)
分析:将玻璃管一端封闭,让玻璃管漂浮在水面上,测出玻璃管浸入水的深度;向玻璃管内倒入一定量的待测液体,用刻度尺测出液体的深度;让玻璃管漂浮在水面上,测出玻璃管浸入水的深度;增大的浮力等于液体的重力,列出关系式即可求出液体的密度.
解答: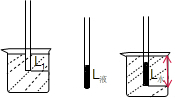 解:实验步骤:
解:实验步骤:
①将橡皮膜紧紧扎在玻璃管的一端,向烧杯中倒入适量水,
把玻璃管放在烧杯中,测出玻璃管进入水中的深度h1;
②在玻璃管中注入适量待测液体,用刻度尺测出液柱高度h液;
③将玻璃管浸于水中,使玻璃管上的橡皮膜处于平衡状态;
用刻度尺测出浸入水中的玻璃管高度h水;
④根据所测数据,计算出ρ液.
(1)设玻璃管的横截面积是S,由阿基米德原理可得:
玻璃管的重力G=F浮=mg=ρ水Sh1g,
玻璃管与液体受到的重力G′=F浮′=ρ水Sh水g,
液体受到的重力G液=G′-G=ρ水Sh水g-ρ水Sh1g,
液体质量m=
=ρ水S(h水-h1),液体体积V=Sh液,
液体密度ρ液=
=
=
.
(2)测量步骤(如图所示):
①将橡皮膜紧紧扎在玻璃管的一端,向烧杯中倒入适量水,
把玻璃管放在烧杯中,测出玻璃管进入水中的深度h1;
②在玻璃管中注入适量待测液体,用刻度尺测出液柱高度h液;
③将玻璃管浸于水中,使玻璃管上的橡皮膜处于平衡状态;
用刻度尺测出浸入水中的玻璃管高度h水;
④根据所测数据,计算出ρ液.
故答案为:(1)ρ液=
.
(2)①将橡皮膜紧紧扎在玻璃管的一端,向烧杯中倒入适量水,
把玻璃管放在烧杯中,测出玻璃管进入水中的深度h1;
②在玻璃管中注入适量待测液体,用刻度尺测出液柱高度h液;
③将玻璃管浸于水中,使玻璃管上的橡皮膜处于平衡状态;
用刻度尺测出浸入水中的玻璃管高度h水;
④根据所测数据,计算出ρ液.如图所示.
 解:实验步骤:
解:实验步骤:①将橡皮膜紧紧扎在玻璃管的一端,向烧杯中倒入适量水,
把玻璃管放在烧杯中,测出玻璃管进入水中的深度h1;
②在玻璃管中注入适量待测液体,用刻度尺测出液柱高度h液;
③将玻璃管浸于水中,使玻璃管上的橡皮膜处于平衡状态;
用刻度尺测出浸入水中的玻璃管高度h水;
④根据所测数据,计算出ρ液.
(1)设玻璃管的横截面积是S,由阿基米德原理可得:
玻璃管的重力G=F浮=mg=ρ水Sh1g,
玻璃管与液体受到的重力G′=F浮′=ρ水Sh水g,
液体受到的重力G液=G′-G=ρ水Sh水g-ρ水Sh1g,
液体质量m=
| G液 |
| g |
液体密度ρ液=
| m |
| V |
| ρ水S(h水-h1) |
| Sh液 |
| ρ水(h水-h1) |
| h液 |
(2)测量步骤(如图所示):
①将橡皮膜紧紧扎在玻璃管的一端,向烧杯中倒入适量水,
把玻璃管放在烧杯中,测出玻璃管进入水中的深度h1;
②在玻璃管中注入适量待测液体,用刻度尺测出液柱高度h液;
③将玻璃管浸于水中,使玻璃管上的橡皮膜处于平衡状态;
用刻度尺测出浸入水中的玻璃管高度h水;
④根据所测数据,计算出ρ液.
故答案为:(1)ρ液=
| ρ水(h水-h1) |
| h液 |
(2)①将橡皮膜紧紧扎在玻璃管的一端,向烧杯中倒入适量水,
把玻璃管放在烧杯中,测出玻璃管进入水中的深度h1;
②在玻璃管中注入适量待测液体,用刻度尺测出液柱高度h液;
③将玻璃管浸于水中,使玻璃管上的橡皮膜处于平衡状态;
用刻度尺测出浸入水中的玻璃管高度h水;
④根据所测数据,计算出ρ液.如图所示.
点评:本题难度很大,没有天平和量筒等常用工具,要想到利用浮力知识,还要利用水这种熟悉的材料,设计出借助玻璃管让液体飘浮在水面上,浮力等于重力才能解出答案.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目