题目内容
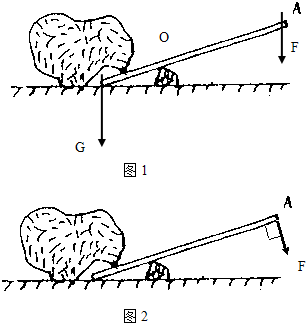 (1)小明用一根木棒撬石头,已知石头重400N,阻力臂长30cm,从支点到动力作用线的距离是1.2m,求作用在木棒上的动力?
(1)小明用一根木棒撬石头,已知石头重400N,阻力臂长30cm,从支点到动力作用线的距离是1.2m,求作用在木棒上的动力?(2)作出杠杆的动力臂和阻力臂,这个杠杆是一个
(3)如图2,如果小明用力的方向发生了改变,则F变大还是变小?为什么?作出杠杆的动力臂F.
分析:(1)知道此题中的阻力、阻力臂和动力臂,据杠杆的平衡条件可以计算出此时的动力.
(2)杠杆的五个要素:
①支点:杠杆绕着转动的点;
②动力:使杠杆转动的力;
③动力臂:从支点到动力作用线的距离;
④阻力:阻碍杠杆转动的力;
⑤阻力臂:从支点到阻力作用线的距离.
当动力臂大于阻力臂时,是省力杠杆;当动力臂小于阻力臂时,是费力杠杆,费力但省距离;当动力臂等于阻力臂时,是等臂杠杆.
(3)图2中,小明动力的方向发生了变化,根据杠杆的平衡条件分析动力的变化,结合动力臂的概念画出动力臂.
(2)杠杆的五个要素:
①支点:杠杆绕着转动的点;
②动力:使杠杆转动的力;
③动力臂:从支点到动力作用线的距离;
④阻力:阻碍杠杆转动的力;
⑤阻力臂:从支点到阻力作用线的距离.
当动力臂大于阻力臂时,是省力杠杆;当动力臂小于阻力臂时,是费力杠杆,费力但省距离;当动力臂等于阻力臂时,是等臂杠杆.
(3)图2中,小明动力的方向发生了变化,根据杠杆的平衡条件分析动力的变化,结合动力臂的概念画出动力臂.
解答:解:(1)石头重即阻力F2=400N,阻力臂L2=30cm;从支点到动力作用线的距离是1.2m,即动力臂L1=1.2m=120cm,由杠杆平衡条件F1L1=F2L2可得:
动力为:F1=
=
=100N.
(2)动力臂是支点到动力作用线的距离,阻力臂是从支点到阻力作用线的距离,如下图所示:
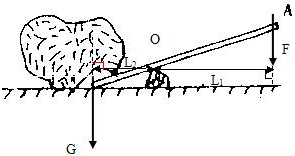
由图可见,动力臂大于阻力臂,因此是省力杠杆,此杠杆的好处是省力,但是费距离,如起子、撬棍等.
(3)如图2,如果小明用力的方向发生了改变,动力方向与杠杆垂直,动力臂如图所示:
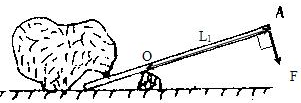
由图可见,动力臂L1变大,阻力和阻力臂不变,根据杠杆的平衡条件:动力×动力臂=阻力×阻力臂,因此动力变小.
故答案为:(1)作用在木棒上的动力为100N;
(2)省力;省力;费距离;起子;
(3)F变小,因为动力臂L1变大,阻力和阻力臂不变,根据杠杆的平衡条件:动力×动力臂=阻力×阻力臂,因此动力变小.
动力为:F1=
| F2×L2 |
| L1 |
| 400N×30cm |
| 120cm |
(2)动力臂是支点到动力作用线的距离,阻力臂是从支点到阻力作用线的距离,如下图所示:

由图可见,动力臂大于阻力臂,因此是省力杠杆,此杠杆的好处是省力,但是费距离,如起子、撬棍等.
(3)如图2,如果小明用力的方向发生了改变,动力方向与杠杆垂直,动力臂如图所示:

由图可见,动力臂L1变大,阻力和阻力臂不变,根据杠杆的平衡条件:动力×动力臂=阻力×阻力臂,因此动力变小.
故答案为:(1)作用在木棒上的动力为100N;
(2)省力;省力;费距离;起子;
(3)F变小,因为动力臂L1变大,阻力和阻力臂不变,根据杠杆的平衡条件:动力×动力臂=阻力×阻力臂,因此动力变小.
点评:本题考查了力臂的作图和杠杆平衡条件的应用,属于基础性题目,解题时要特别注意.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 (2009?南京模拟)
(2009?南京模拟) 小明按下列步骤测量固态烛蜡的密度:
小明按下列步骤测量固态烛蜡的密度: 小明用一根木棒撬石头,已知石头重400N,阻力臂长30cm,从支点到动力作用线的距离是1.2m,求作用在木棒上的动力?作出图中杠杆所受各力的力臂.
小明用一根木棒撬石头,已知石头重400N,阻力臂长30cm,从支点到动力作用线的距离是1.2m,求作用在木棒上的动力?作出图中杠杆所受各力的力臂.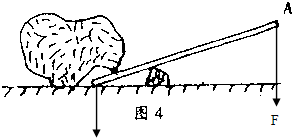 小明用一根木棒撬石头,已知石头重400N,阻力臂长30cm,从支点到动力作用线的距离是1.2m,求作用在木棒上的动力?作出图中杠杆所受各力的力臂.
小明用一根木棒撬石头,已知石头重400N,阻力臂长30cm,从支点到动力作用线的距离是1.2m,求作用在木棒上的动力?作出图中杠杆所受各力的力臂.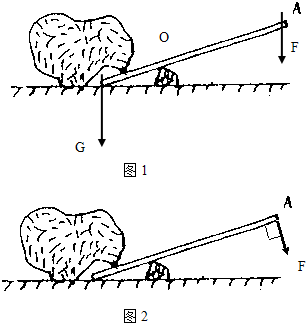 (1)小明用一根木棒撬石头,已知石头重400N,阻力臂长30cm,从支点到动力作用线的距离是1.2m,求作用在木棒上的动力?
(1)小明用一根木棒撬石头,已知石头重400N,阻力臂长30cm,从支点到动力作用线的距离是1.2m,求作用在木棒上的动力?