题目内容
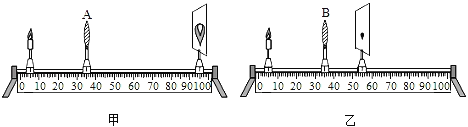
【题目】如图甲所示,柱状容器内放入一个体积大小为160cm3的长方体木块且容器足够高,现不断向容器内注入水,并记录木的总体积V和所对应的水的深度h,V和h的对应关系如图乙所示.则长方体木块的底面积S1为cm2 , 物体的密度为kg/m2 . 
【答案】8;0.75×103
【解析】解:(1)由表中数据可知,h从5﹣10cm,水的体积变化: △V=(S2﹣S1)(10cm﹣5cm)=60cm3 , ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
h从18﹣21cm,水的体积变化:
△V′=S2(h5﹣h4)=60cm3 ,
即:S2(21cm﹣18cm)=60cm3 ,
解得:S2=20cm2 ,
代入①得:S1=8cm2;(2)由于长方体木块的体积V木=S1H,则柱状物体的高:
H= ![]() =
= ![]() =20cm;
=20cm;
如果长方体木块的密度大于或等于水的密度,在加水过程中长方体木块将静止在容器底不会上浮,容器内水的体积变化在20cm以内应该与h的变化成正比;
由图象数据可知器内水的体积变化应该与h的变化不成正比,所以长方体木块的密度小于水的密度;因此随着水的增多,长方体木块将漂浮在水面上,
设长方体木块浸入的深度为H浸 ,
当h5=21cm时,
水的体积:
S2h5﹣S1H浸=300cm3 ,
即:20cm2×21cm﹣8cm2×H浸=300cm3 ,
解得:
H浸=15cm,
此时排开水的体积:
V排=S1H浸=8cm2×15cm=120cm3 ,
由于长方体木块漂浮,则F浮=G木 ,
即:ρ水V排g=ρ木Vg,
所以,1×103kg/m3×120cm3×g=ρ木×160cm3×g,
解得:
ρ木=0.75×103kg/m3 .
所以答案是:8;0.75×103 .
【考点精析】本题主要考查了阿基米德原理和物体的浮沉条件及其应用的相关知识点,需要掌握阿基米德原理:浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开的液体所受的重力.这个规律叫做阿基米德原理,即 F浮= G排 =ρ液gv排;物体的浮沉条件:浸没在液体中的物体 F浮>G 时上浮,F浮 = G 时悬浮,F浮 <G 时下沉.物体浮沉条件的应用举例:(1)轮船(2)潜水艇(3)气球(4)飞艇、热气(5)密度计(密度计的刻度是从上到下刻度变大,刻度不均匀,且刻度无单位.)才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】黎黎同学配制了一定浓度的盐水,棒妈妈筛选出饱满的种子,她想知道所配制出的盐水密度,就用天平和量筒来进行测量. 
(1)把天平放在上,将拨到标尺左端的零刻线处后,发现天平横梁左高右低,应将平衡螺母向调节,使天平平衡.
(2)用调节好的天平测得空烧杯的质量m1; 把适量的盐水倒入量筒中,测得盐水体积V,如图甲所示;
把量筒中的盐水倒入烧杯中,测得烧杯和盐水的总质量m2 , 如图乙所示.根据图中数据,帮黎黎同学把表填写完整:
空烧杯的质量 | 量筒中盐水的体积 | 烧杯和盐水的总质量 | 盐水的密度 |
30 |
(3)以上方法测出的盐水密度值比真实值 . (选填“偏大”或“偏小”)
(4)黎黎同学发现混杂在种子中的小石块也同饱满的种子一起沉入了盐水底部,她想尽快知道石块的密度究竟有多大,就选了一块大小合适且与其材质相同的石块,巧妙利用图乙所示的天平状态,按以下的步骤测出了石块的密度. ①用细线栓着石块浸没在盐水中(石块未接触烧杯底且盐水未溢出),天平的读数增大了△m1
②将石块缓慢沉入烧杯底部,放开细线,天平的读数再增大了△m2;
③石块密度的表达式ρ石=(用△m1 , △m1及盐水密度ρ表示)