题目内容
（2012?泰州模拟）如图所示，均匀的长方形薄片合金电阻板abcd，ab边为L1，ad边为L2，当端点1、2或3、4接入电路时，R12：R34=L22：L21
L22：L21
．分析：①由电阻定律可知，导体的电阻R与它的长度L成正比，与它的横截面积S成反比，还与导体的材料有关系，公式为：R=ρ?
（其中ρ为电阻的材料电阻率）．
②设导体的厚度为d，则导体的横截面积为Ld，当把端点1、2接入电路时，导体的长度为L2，当把端点3、4接入电路时，导体的长度为L1，从而可以利用公式R=ρ?
计算出R12：R34的比值．
| L |
| S |
②设导体的厚度为d，则导体的横截面积为Ld，当把端点1、2接入电路时，导体的长度为L2，当把端点3、4接入电路时，导体的长度为L1，从而可以利用公式R=ρ?
| L |
| S |
解答：解：设导体的厚度为d，
当把端点1、2接入电路时，而ab边为L1，
则此时导体的横截面积为：S12=L1d，
而此时导体的长度为L2，
∴R12=ρ?
=ρ?
；
当把端点3、4接入电路时，而ad边为L2，
则此时导体的横截面积为：S34=L2d，
而此时导体的长度为L1，
∴R34=ρ?
=ρ?
；
则，R12：R34=ρ?
：ρ?
=
：
，
即：R12：R34=L22：L21．
当把端点1、2接入电路时，而ab边为L1，
则此时导体的横截面积为：S12=L1d，
而此时导体的长度为L2，
∴R12=ρ?
| L2 |
| S12 |
| L2 |
| L1d |
当把端点3、4接入电路时，而ad边为L2，
则此时导体的横截面积为：S34=L2d，
而此时导体的长度为L1，
∴R34=ρ?
| L1 |
| S34 |
| L1 |
| L2d |
则，R12：R34=ρ?
| L2 |
| L1d |
| L1 |
| L2d |
| L2 |
| L1 |
| L1 |
| L2 |
即：R12：R34=L22：L21．
点评：本题考查了学生对电阻定律R=ρ?
（其中ρ为电阻的材料电阻率）的理解和应用，本题的关键是对导体长度的判断．
| L |
| S |
练习册系列答案
相关题目
（2012?泰州模拟）在图中根据小磁针静止时的指向标出通电螺线管的两极和电源的正负极．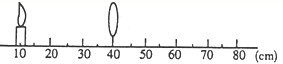
（2012?泰州模拟）小丽在探究凸透镜成像规律时，使用的透镜焦距为10cm，它们把蜡烛和凸透镜分别放在如图所示位置，然后调节光屏至合适的位置，则显示一个倒立、