题目内容
一颗炸弹在海面上某处发生爆炸,过了一会站在岸边的人听到了第一次爆炸声,又经过时间△t他再次听到爆炸声,当时声音在空气中和海水中的传播速度分别为v1和v2,那么岸边的人距离爆炸处的距离为
- A.(v2-v1)△t
- B.v1v2△t/v2-v1
- C.v1v2△t/v1-v2
- D.(v1v2)△t
B
分析:站在岸上的人听到两次爆炸声,第一次是通过水传播的,第二次是通过空气传播的,因为两次传播的路程相同,水的传声速度大于空气传声速度,求出传播时间,根据两次传声有个时间差列出等式,求出人距离爆炸处的距离.
解答:设人和爆炸处的距离为s,
所以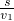 -
-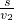 =△t,
=△t,
整理得,s=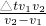 .
.
故选B.
点评:根据速度公式变形求出两次传播时间,根据时间差列出等式求出距离.
分析:站在岸上的人听到两次爆炸声,第一次是通过水传播的,第二次是通过空气传播的,因为两次传播的路程相同,水的传声速度大于空气传声速度,求出传播时间,根据两次传声有个时间差列出等式,求出人距离爆炸处的距离.
解答:设人和爆炸处的距离为s,
所以
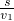 -
-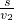 =△t,
=△t,整理得,s=
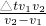 .
.故选B.
点评:根据速度公式变形求出两次传播时间,根据时间差列出等式求出距离.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目