题目内容
将质量为m0的一小杯热水倒入盛有质量为m的冷水的保温容器中,使得冷水温度升高了3℃,然后又向保温容器中倒入一小杯同质量同温度的热水,水温又上升了2.8℃.不计热量的损失,则可判断
- A.热水和冷水的温度差为87℃,m0:m=1:28
- B.热水和冷水的温度差为69℃,m0:m=1:32
- C.热水和冷水的温度差为54T:,m0:m=1:24
- D.热水和冷水的温度差为48℃,m0:m=1:20
A
分析:热传递过程中高温物体放出热量,低温物体吸收热量,直到最后温度相同.
设热水和冷水的温度差为t,知道热水的质量和温度变化、冷水的质量和温度变化,利用热平衡方程Q吸=Q放列出两个等式,进行解答即可.
解答:设热水和冷水的温度差为t,
∵质量为m0的一小杯热水倒入盛有质量为m的冷水的保温容器中,使得冷水温度升高了3℃,
∴Q吸=Q放,
从而可知,cm0(t-3℃)=cm×3℃,①
又向保温容器中倒入一小杯同质量为m0同温度的热水,水温又上升了2.8℃,
∴Q吸=Q放,
从而可知,cm0(t-3℃-2.8℃)=c(m+m0)×2.8℃,②
则①-②得:
2.8℃cm0=3℃cm-2.8℃cm-2.8℃cm0,
整理得:5.6℃cm0=0.2℃cm,
∴ =
= =
=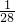 ,即m=28m0,
,即m=28m0,
把它代入①式得:
cm0(t-3℃)=c×28m0×3℃,
解得:t=87℃.
故选A.
点评:解决此类综合分析题目,要结合热量公式和热传递的条件进行分析解答.不计热量的损失,可利用热平衡方程Q吸=Q放列出两个等式,进行解答即可.
分析:热传递过程中高温物体放出热量,低温物体吸收热量,直到最后温度相同.
设热水和冷水的温度差为t,知道热水的质量和温度变化、冷水的质量和温度变化,利用热平衡方程Q吸=Q放列出两个等式,进行解答即可.
解答:设热水和冷水的温度差为t,
∵质量为m0的一小杯热水倒入盛有质量为m的冷水的保温容器中,使得冷水温度升高了3℃,
∴Q吸=Q放,
从而可知,cm0(t-3℃)=cm×3℃,①
又向保温容器中倒入一小杯同质量为m0同温度的热水,水温又上升了2.8℃,
∴Q吸=Q放,
从而可知,cm0(t-3℃-2.8℃)=c(m+m0)×2.8℃,②
则①-②得:
2.8℃cm0=3℃cm-2.8℃cm-2.8℃cm0,
整理得:5.6℃cm0=0.2℃cm,
∴
 =
= =
=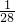 ,即m=28m0,
,即m=28m0,把它代入①式得:
cm0(t-3℃)=c×28m0×3℃,
解得:t=87℃.
故选A.
点评:解决此类综合分析题目,要结合热量公式和热传递的条件进行分析解答.不计热量的损失,可利用热平衡方程Q吸=Q放列出两个等式,进行解答即可.

练习册系列答案
相关题目