题目内容
【题目】“测量小灯泡电功率”的实验中,电源为两节新干电池,电压为3V,小灯泡的额定电压为2.5V,正常发光时灯丝电阻约为10Ω,所用滑动变阻器的最大阻值20Ω.
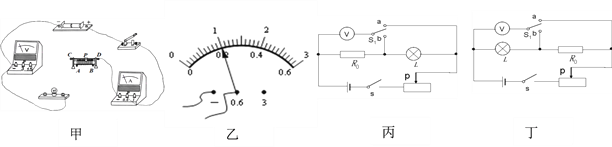
(1)请用笔画线代替导线在图甲中完成实物电路的连接(要求滑片向B滑动时,接入电路阻值减小,且导线不能交叉) ________.
(2)实验时,某个小组同学刚闭合开关就发现小灯泡亮度很亮然后马上熄灭了,老师指出了同学们操作时的错误是__,同时提醒同学们注意观察此时电表的示数,发现电流表无示数,电压表__________(选填“有示数”, “ 无示数”).
(3)断开开关,更换了相同规格的小灯泡后重新按照正确的操作进行实验.移动滑片,当灯正常发光时,电流表示数如图乙所示,小灯泡的额定电流为___A,小灯泡的额定功率是___W, 小灯泡正常发光的电阻是__Ω.
(4)小华打算增加一个阻值为10Ω的定值电阻R0,只利用一只电压表,通过图中操作(开关S接“a”“b”各一次)来测量小灯泡的额定功率.图丙、丁是她设计的两种不同方案的电路图,则以下判断正确的是____.
A.两种方案都能
B.两种方案都不能
C.丙方案能,丁方案不能
D.丙方案不能,丁方案能
(5)小华还想探究“在电压一定的情况下,电流与电阻的关系”,于是将甲图中的小灯泡换成四个阻值分别为10Ω, 8Ω, 6Ω和4Ω的定值电阻,其余连接均不改变.在实验过程中,将4个定值电阻依次接入电路,调节滑动变阻器使定值电阻两端的电压保持某个值U0不变,为了能够顺利得到4组I 、R数据,完成实验,该电压U0的取位大小应满足:___________ ;完成实验后,小华分析数据得到:在电压一定的情况下,___________的结论.
(6)完成实验后,小华想用原电路测某一定值电阻Rx的阻值,他用该电阻替换灯泡后,发现电压表损坏了,便将其拆除.若滑动变阻器的最大阻值用R0表示,你在不改变其他元件连接的方式下,帮他完成实验:(几次实验后,电池电压稍有下降)
实验步骤:A._______________________________________;
B._______________________________________;表达式:_______________(用所测物理量符号表示).
【答案】 闭合开关前,未将滑片P移至最大阻值处 有示数 0.2 0.5 12.5 D 1V≤U0≤2.4V 电流与电阻成反比 滑片移至阻值最大处,记下电流表的示数Ib 将滑片移至阻值最小处 记下电流表的示数Ia Rx=![]()
![]()
【解析】(1)在“测量小灯泡电功率”的实验中,小灯泡与滑动变阻器串联,要求滑片向B滑动时,接入电路阻值减小,即PB段电阻丝接入电路,接线柱B连入电路;电压表并联在小灯泡两端,选用量程0~3V。连线如下:
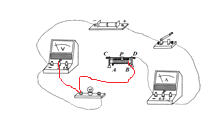
(2)实验时,某个小组同学刚闭合开关就发现小灯泡亮度很亮然后马上熄灭了,同学们操作时的错误是闭合开关前,未将滑片P移至最大阻值处。注意观察此时电表的示数,发现电流表无示数,电压表有示数。
(3)当灯正常发光时,电流表示数如图乙所示,小灯泡的额定电流为I额=0.2A,小灯泡的额定功率是P额=U额I额=2.5V×0.2A=0.5W;
小灯泡正常发光时的电阻 ![]()
(4)在丁图中,S拨到b,电压表测灯的电压,移动滑片使灯的电压为UL=2.5V,灯正常发光,保持滑片的位置不动,将S拨到a,电压表测灯与定值电阻的总电压ULR0,因电路的连接没有改变,各电阻大小和电压不变,根据串联电路电压的规律,定值电阻的电压UR0=ULR0-2.5V,根据欧姆定律可求通过定值电阻的电流,根据串联电路电流的特点即灯正常发光的电路,根据PL=ULIL可求灯的额定功率;
图丙中,S拨到b,电压表定值电阻的电压,S拨到a,电压表测灯与定值电阻的电压,无法确定灯泡是否正常发光,故丙方案不能,丁方案能。答案为D。
(5)把四个电阻分别串联接入电路中,为了保护电流表,电路中的电流不能超过0.6A,故电路的最小电阻![]() ,
,
电路中接入4Ω的电阻时,滑动变阻器接入电路的最小电阻为:R滑小=R小-4Ω=1Ω;根据串联电路电压的规律,当电压表示数为U0时,变阻器分得的电压U滑=U-U0=3V-U0,
根据分压原理: ![]() ,即
,即![]() ,因为探究电流与电阻关系时,应保持定值电阻两端的电压U0为定值,所以等式左边为定值,右边也为定值,当R滑最小为1Ω时,对应的定值电阻为4Ω,代入上式得:U0=2.4V,即定值电阻两端的最大电压为2.4V。
,因为探究电流与电阻关系时,应保持定值电阻两端的电压U0为定值,所以等式左边为定值,右边也为定值,当R滑最小为1Ω时,对应的定值电阻为4Ω,代入上式得:U0=2.4V,即定值电阻两端的最大电压为2.4V。
当定值电阻为最大10Ω时,同理,对应的变阻器有最大值R滑大=20Ω,代入上式得:U0=1V,即1V≤U0≤2.4V
分析数据得到:在电压一定的情况下,电流与电阻成反比的结论。
(6)实验步骤:
A.滑片移至阻值最大处,记下电流表的示数Ib ,
B.将滑片移至阻值最小处 ,记下电流表的示数Ia ,
因电源的电压不变,所以,U=IaRx=Ib(Rx+R0)
解得: ![]() .
.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案