题目内容
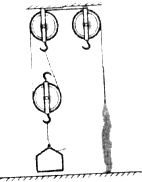
【题目】工人用如图所示的滑轮组和竹筐把质量为1t的沙子提升到高处．已知竹筐能承受的最大压强为3000Pa，竹筐的底面积为3600cm2，工人提空筐上去时用力大小为60N，g=10N/kg，不计绳重和摩擦．求：
（1）工人提升880N的沙子上升了3m，用时30s，则工人做功的功率是多少？
（2）在保证安全的情况下，工人每次提升多重的沙子，装置的机械效率最大？为多少？
（3）若把全部沙子提升到3m高处，工人至少要做多少额外功？
【答案】（1）工人提升880N的沙子上升了3m，用时30s，则工人做功的功率是100W；
（2）在保证安全的情况下，工人每次提升1080N的沙子，装置的机械效率最大，此时装置的机械效率是90%；
（3）若把全部的沙子提升到3m高处，则工人至少要做额外功3600J
【解析】
试题分析：（1）已知动滑轮上有两端绳子，先求出动滑轮和空筐的重力，再求出提升880N沙子时绳端拉力大小，最后利用公式P=Fv求出功率的大小；
（2）先求出一次能提升沙子的最大重力，再利用公式η=
=
求出机械效率的大小；
（3）先求出把1t的沙子提完，则至少要提多少次，再求出每一次的额外功大小，最后求出都提完总共做的额外功大小．
解：（1）由图可知，n=2；
不计绳重和摩擦，提升空筐时，拉力F=
，
所以G动+G筐=2F=2×60N=120N，
提升880N沙子时，绳端的拉力：F′=
=
=500N，
重物移动的速度：v物=
=
=0.1m/s，
工人做功的功率：
P=F′v绳=F′nv物=500N×2×0.1m/s=100W；
（2）一次能提升沙子的最大重力：
G沙′=F=pS=3000Pa×3600×10﹣4m2=1080N，此时滑轮组的机械效率最大，
滑轮组的最大机械效率：
η=
=
=
=
×100%=90%；
（3）要把1t的沙子提完，至少要提升的次数：
n=
=
=9.26，
所以要把1t的沙子提完，则至少要提10次．
每一次所做的额外功：W额=（G动+G筐）h=120N×3m=360J，
所以，要提完1t的沙子总共做的额外功为：W额总=360J×10=3600J．
答：（1）工人提升880N的沙子上升了3m，用时30s，则工人做功的功率是100W；
（2）在保证安全的情况下，工人每次提升1080N的沙子，装置的机械效率最大，此时装置的机械效率是90%；
（3）若把全部的沙子提升到3m高处，则工人至少要做额外功3600J．
