题目内容
用密度为2.7×103千克/米3的铝制成甲、乙、丙三个大小不同的正方体，要求它们的边长分别为0.1米、0.2米和0.3米．制成后经质量检验员称得它们的实际质量分别为3千克、21.6千克和54千克．质量检验员指出：有两个不合格，其中一个掺入了杂质为次品，另一个混入了空气泡的为废品，则下列断正确的是（ ）
分析：先分别算出甲、乙、丙三个正方体的体积，然后用它们的质量除以它们的体积算出它们各自的密度，最后将算得的密度与铝的密度进行比较：相等的为合格品，比铝的密度小的是废品（混入空气，则在相同体积情况下，质量会变小，所以密度会变小），剩下的那一个就是次品．
解答：解：甲的体积：V甲=0.1m×0.1m×0.1m=0.001m3，则甲的密度：ρ甲=
=
=3×103kg/m3；
乙的体积：V乙=0.2m×0.2m×0.2m=0.008m3，则乙的密度：ρ乙=
=
=2.7×103kg/m3；
丙的体积：V丙=0.3m×0.3m×0.3m=0.027m3，则丙的密度：ρ丙=
=
=2×103kg/m3．
因为ρ乙=ρ铝，所以乙是合格品；因为ρ丙＜ρ铝，所以丙是废品；因为ρ甲＞ρ铝，所以甲是次品．
故选C．
| m甲 |
| V甲 |
| 3kg |
| 0.001m3 |
乙的体积：V乙=0.2m×0.2m×0.2m=0.008m3，则乙的密度：ρ乙=
| m乙 |
| V乙 |
| 21.6kg |
| 0.008m3 |
丙的体积：V丙=0.3m×0.3m×0.3m=0.027m3，则丙的密度：ρ丙=
| m丙 |
| V丙 |
| 54kg |
| 0.027m3 |
因为ρ乙=ρ铝，所以乙是合格品；因为ρ丙＜ρ铝，所以丙是废品；因为ρ甲＞ρ铝，所以甲是次品．
故选C．
点评：因为密度是物质的一种特性，所以我们可以利用密度来鉴别物质．解答该题的思路就是分别算出三个正方体的密度，然后和铝的密度进行比较．
练习册系列答案
阅读快车系列答案
相关题目
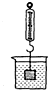如图所示，烧杯内盛有某种液体，把一体积为1×10-4m3的铝块用细线系在弹簧测力计下浸没在液体中，静止时弹簧测力计的示数为1.5N，已知铝的密度为2.7×1O3kg/m3．则铝块在液体中受到的浮力等于
（2011?平谷区二模）如图是小刚用滑轮组提升水中铝块的示意图．当铝块浸没在水面以下匀速上升时，作用在绳子自由端的拉力为F1，小刚对地面的压强为P1，滑轮组的机械效率为η1；当铝块的上表面露出水面20cm时，作用在绳子自由端的拉力为F2，小刚对地面的压强为P2，滑轮组的机械效率为η2；当铝块全部露出水面后匀速上升时，作用在绳子自由端的拉力为F3，小刚对地面的压强为P3，滑轮组的机械效率为η3；已知滑轮组中大小两种滑轮的质量之比为3：1，小刚身体的质量为60kg，圆柱形铝块的底面积为0.06m2，铝的密度为2.7×103kg/m3，若F1：F2=5：6，P1：P3=10：9，（不计水的阻力、绳重和摩擦，g取10N/kg），求：