题目内容
如图所示,OB为一轻质杠杆,可绕O点作自由转动,在杠杆A点和B点分别作用两个力F1和F2(F2未画出)时,恰能使杠杆在水平位置上平衡,已知OA=1cm,OB=3cm.(1)若F1=18N,方向竖直向下,则F2的最小值是多大?
(2)若F1减小为9N,不改变(1)中F2的作用点和最小值的大小,只改变F2的方向,要使杠杆仍在水平位置平衡,则L2为多大?并在图中画出F2的方向.(2种情况)
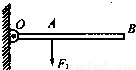
【答案】分析:(1)杠杆在水平位置上平衡,F1的力臂为OA,要使F2最小,F2的力臂需要最大,当在B点竖直向上施加力,此时力臂最大,用力最小,根据杠杆平衡条件求F2的最小值;
(2)只改变F1的大小,不改变方向,F1的力臂不变;不改变(1)中F2的作用点和最小值的大小,F2的大小不变、力臂变化,根据杠杆的平衡条件求F2的力臂,并画出力臂.
解答:解:
(1)由题知,F1的力臂OA=1cm,而F2的最大力臂为OB=3cm,
∵杠杆平衡,
∴F1L1=F2L2;
即:18N×1cm=F2×3cm,
∴F2=6N;
(2)要使杠杆仍能平衡,则应改变F2的方向,使杠杆的受力仍能满足杠杆的平衡条件:
F1′L1=F2L2′;
则可求得F2的力臂为:
L2′=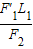 =
=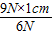 =1.5cm,F2的方向应该与OB成30°,有两种情况,如图所示.
=1.5cm,F2的方向应该与OB成30°,有两种情况,如图所示.
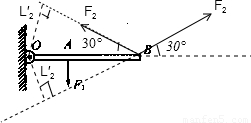
答:(1)F2的最小值为6N;(2)F2的力臂L2为1.5cm,方向如图所示.
点评:本题考查学生对杠杆的平衡条件的应用,在解题时应通过审题找出有用的信息,找出动力、动力臂、阻力、阻力臂中的不变量、变化量是本题的关键.
(2)只改变F1的大小,不改变方向,F1的力臂不变;不改变(1)中F2的作用点和最小值的大小,F2的大小不变、力臂变化,根据杠杆的平衡条件求F2的力臂,并画出力臂.
解答:解:
(1)由题知,F1的力臂OA=1cm,而F2的最大力臂为OB=3cm,
∵杠杆平衡,
∴F1L1=F2L2;
即:18N×1cm=F2×3cm,
∴F2=6N;
(2)要使杠杆仍能平衡,则应改变F2的方向,使杠杆的受力仍能满足杠杆的平衡条件:
F1′L1=F2L2′;
则可求得F2的力臂为:
L2′=
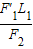 =
=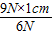 =1.5cm,F2的方向应该与OB成30°,有两种情况,如图所示.
=1.5cm,F2的方向应该与OB成30°,有两种情况,如图所示.
答:(1)F2的最小值为6N;(2)F2的力臂L2为1.5cm,方向如图所示.
点评:本题考查学生对杠杆的平衡条件的应用,在解题时应通过审题找出有用的信息,找出动力、动力臂、阻力、阻力臂中的不变量、变化量是本题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

 18、如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡时,在A点至少需加
18、如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡时,在A点至少需加 如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡时,在A点需加
如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡时,在A点需加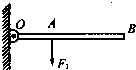 如图所示,OB为一轻质杠杆,可绕O点作自由转动,在杠杆A点和B点分别作用两个力F1和F2(F2未画出)时,恰能使杠杆在水平位置上平衡,已知OA=1cm,OB=3cm.
如图所示,OB为一轻质杠杆,可绕O点作自由转动,在杠杆A点和B点分别作用两个力F1和F2(F2未画出)时,恰能使杠杆在水平位置上平衡,已知OA=1cm,OB=3cm. 如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡时,在A点至少需加
如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡时,在A点至少需加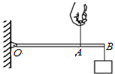 如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡时,在A点至少需加
如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡时,在A点至少需加