题目内容
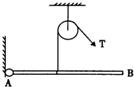
如图,轻绳的一端系有质量为2kg的物体C,另一端系在质量为1kg的均匀木棒AB的A端;木棒AB可绕B端无摩擦转动,在水平拉力F的作用下木棒AB与墙面的夹角由30°增大到60°(g=10N/kg),则( )

| A.拉力F的大小一直不变 | ||||
B.当棒与墙面成30°时拉力F=
| ||||
| C.当棒与墙面成45°时拉力F=25N | ||||
D.当棒与墙面成60°时拉力F=
|

GC=2kg×10N/kg=20N;G木=1kg×10N/kg=10N;
设木棒AB的长度为l,当棒与墙面成30°时,力与力臂的关系如图所示:
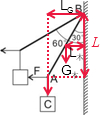
根据直角三角形的关系可知,L=
l,LG=
l,L木=
l;
根据杠杆平衡的条件可得,F×
l=20N×
l+10N×
l,化简可得:F=
N,故B错误;
同理,当棒与墙面成45°时,L=
l,LG=
l,L木=
l;
根据杠杆平衡的条件可得,F×
l=20N×
l+10N×
l,化简可得:F=25N,故C正确;故A错误;
同理,当棒与墙面成60°时,L=
l,LG=
l,L木=
l;
根据杠杆平衡的条件可得,F×
l=20N×
l+10N×
l,化简可得:F=
N,故D错误.
故选C.
设木棒AB的长度为l,当棒与墙面成30°时,力与力臂的关系如图所示:

根据直角三角形的关系可知,L=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
根据杠杆平衡的条件可得,F×
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
25
| ||
| 3 |
同理,当棒与墙面成45°时,L=
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
根据杠杆平衡的条件可得,F×
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
同理,当棒与墙面成60°时,L=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
根据杠杆平衡的条件可得,F×
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
25
| ||
| 2 |
故选C.

练习册系列答案
相关题目