Question

有一天，小明在家观察洗衣机排水后，对容器排尽水的时间与排水孔的大小之间的关系产生了浓厚的兴趣．为此他找来四个同样大小的圆柱形塑料容器，在它们的底部相同位置各开一个排水圆孔，排水孔的直径d分别是1.5cm、2．Ocm、3．Ocm和5．Ocm．在容器里放入30cm深的水，打开排水孔让水流出，用秒表测量水完全流出所需的时间t分别为73．Os、41.2s、18.4s和6.8s．
（1）请设计一个表格，并将小明测得的数据填写在表格中．
（2）请在右图中画出排尽水的时间t与排水孔直径d的关系图线．
（3）分析实验数据，初步可以看出t与d之间的关系为：d越大，t

 

，但是还不能确定它们之间明确的数量关系．
（4）请你猜想t与d之间可能存在的数量关系，并根据以上数据写出证实你猜想的思路．
猜想：

 

；
思路：

 

．

Answer 1

分析：（1）由探究容器排水时间与排水孔大小的实验可知：变量是排尽水的时间t，自变量是排水孔直径d，所以设计的表格就是这两个变量的数据表格．
（2）作图象时，先在坐标中找出各点对应的坐标，然后用平滑的曲线连接各点，即可得到排水时间t与排水孔直径d的关系图线．
（3）根据实验数据，d越大，t的数据变化大致趋势即可．
（4）为明确t与d之间可能存在的数量关系，可根据数据变化猜想．

解答：解：（1）数据表格中需要记录的数据是：排尽水的时间t、排水孔直径d，所以设计的表格如下：

排水孔直径d/cm	1.5	2	3	5
排尽水的时间t/s	73.0	41.2	18.4	6.8

（2）按照先在坐标中找出各点对应的坐标，然后用平滑的曲线连接各点的原则；
做出的关系图线如图

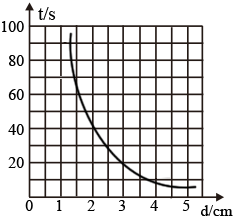
（3）由实验数据可知：排水孔直径d越大时，排尽水的时间t由73.0s变化为6.8s，所以t是越小了．
（4）因为t与d之间的变化关系是随d增大，t越来越小，而影响排水时间的主要是孔的面积，所以猜想是：排水时间t与d²成反比；
由于成反比的曲线图象不便于观察判断，所以可以通过作出t与

1

d2

图线，并观察图线是否为一条直线来判断．
故答案：（3）越小；（4）t与d²成反比；可以作出t与

1

d2

图线，并观察图线是否为一条直线．

点评：本题考查实验的整个探究过程，但是注意猜想和实验设计的合理性．