题目内容
某人用10牛的拉力,沿斜面将重为16牛的物体匀速地拉上长为4米,高为2米的斜面顶端.该斜面的机械效率η及斜面对物体的摩擦力f大小分别为
- A.η=O.5,f=8牛
- B.η=O.5,f=2牛
- C.η=0.8,f=8牛
- D.η=O.8,f=2牛
D
分析:已知物体重力和提升的高度,根据公式W=Gh可求有用功,根据公式W=Fs可求总功,机械效率等于有用功除以总功;
求出额外功,而W额=fs,据此求摩擦力大小.
解答:W有用=Gh=16N×2m=32J,
W总=Fs=10N×4m=40J,
η= =
= =80%;
=80%;
∵W总=W有用+W额,
∴W额=W总-W有用=40J-32J=8J,
∵W额=fs,
∴f=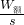 =
= =2N.
=2N.
故选D.
点评:本题考查了有用功、总功、额外功、机械效率的计算,知道利用斜面时做的额外功就是克服摩擦做功是本题的关键.
分析:已知物体重力和提升的高度,根据公式W=Gh可求有用功,根据公式W=Fs可求总功,机械效率等于有用功除以总功;
求出额外功,而W额=fs,据此求摩擦力大小.
解答:W有用=Gh=16N×2m=32J,
W总=Fs=10N×4m=40J,
η=
 =
= =80%;
=80%;∵W总=W有用+W额,
∴W额=W总-W有用=40J-32J=8J,
∵W额=fs,
∴f=
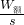 =
= =2N.
=2N.故选D.
点评:本题考查了有用功、总功、额外功、机械效率的计算,知道利用斜面时做的额外功就是克服摩擦做功是本题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目