题目内容
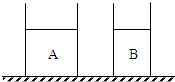 如图所示,两个底面积不同的圆柱形容器内分别盛有不同的液体A和B,已知两容器内液面等高,且液体的质量相等.现将实心金属球甲浸没在液体A中、实心金属球乙浸没在液体B中,均无液体溢出,这时A、B两液体对容器底部的压强大小相等,则
如图所示,两个底面积不同的圆柱形容器内分别盛有不同的液体A和B,已知两容器内液面等高,且液体的质量相等.现将实心金属球甲浸没在液体A中、实心金属球乙浸没在液体B中,均无液体溢出,这时A、B两液体对容器底部的压强大小相等,则
- A.甲的体积小于乙的体积
- B.甲的体积大于乙的体积
- C.甲的质量小于乙的质量
- D.甲的质量大于乙的质量
B
分析:由题意知液体体积不同VA>VB,质量相同,则体积大的密度小,即ρA<ρB.现在两液体对容器底的压强相等,
由于压强P=ρgh,则hA>hB.原来两液面等高,放入球后hA>hB,从而可推知甲的体积大于乙的体积.
解答:由题干可知两圆柱形容器的底面积SA>SB,两容器内液面等高hA=hB,所以液体体积V=Sh,不同VA>VB.两液体的质量m=ρV相等,所以两液体密度不同,ρA<ρB.
两实心球完全浸没在液体中,两液体对容器底部压强相等,即PA=PB,液体对容器底部的压强P=ρgh,所以ρAgh′A=ρBg h′B,因为ρA<ρB,所以h′A>h′B.
放入液体中球的体积等于球排开液体的体积V甲=SA(h′A-hA),V乙=SB(h′B-hB),因为SA>SB,hA=hB,h′A>h′B,所以V甲>V乙.
故选B.
点评:这是一道推理判断题,球的体积等于球所排开液体的体积,先判断两液体的密度大小,再由液体对容器底的压强相等判断两液体的高度关系,最后求球所排开液体的体积,即球的体积.
分析:由题意知液体体积不同VA>VB,质量相同,则体积大的密度小,即ρA<ρB.现在两液体对容器底的压强相等,
由于压强P=ρgh,则hA>hB.原来两液面等高,放入球后hA>hB,从而可推知甲的体积大于乙的体积.
解答:由题干可知两圆柱形容器的底面积SA>SB,两容器内液面等高hA=hB,所以液体体积V=Sh,不同VA>VB.两液体的质量m=ρV相等,所以两液体密度不同,ρA<ρB.
两实心球完全浸没在液体中,两液体对容器底部压强相等,即PA=PB,液体对容器底部的压强P=ρgh,所以ρAgh′A=ρBg h′B,因为ρA<ρB,所以h′A>h′B.
放入液体中球的体积等于球排开液体的体积V甲=SA(h′A-hA),V乙=SB(h′B-hB),因为SA>SB,hA=hB,h′A>h′B,所以V甲>V乙.
故选B.
点评:这是一道推理判断题,球的体积等于球所排开液体的体积,先判断两液体的密度大小,再由液体对容器底的压强相等判断两液体的高度关系,最后求球所排开液体的体积,即球的体积.

练习册系列答案
相关题目
 (2011?青浦区一模)如图所示,两个底面积不同的圆柱形容器内分别盛有不同的液体甲和乙,甲液体的质量大于乙液体的质量.下列措施中,有可能使两容器内液体对容器底部的压强相等的是(无液体溢出)( )
(2011?青浦区一模)如图所示,两个底面积不同的圆柱形容器内分别盛有不同的液体甲和乙,甲液体的质量大于乙液体的质量.下列措施中,有可能使两容器内液体对容器底部的压强相等的是(无液体溢出)( ) (2011?卢湾区二模)如图所示,两个底面积不同的圆柱形容器A和B(SA>SB),容器足够高,分别盛有甲、乙两种液体,且两种液体对容器底部的压强相等.若在A容器中倒入或抽出甲液体,在B容器中倒入或抽出乙液体,使两种液体对容器底部的压力相等,正确的判断是( )
(2011?卢湾区二模)如图所示,两个底面积不同的圆柱形容器A和B(SA>SB),容器足够高,分别盛有甲、乙两种液体,且两种液体对容器底部的压强相等.若在A容器中倒入或抽出甲液体,在B容器中倒入或抽出乙液体,使两种液体对容器底部的压力相等,正确的判断是( ) (2013?太仓市模拟)如图所示,两个底面积不同的圆柱形容器内分别盛有深度不同的液体,已知距容器底部均为h的A、B两点的压强相等.现将实心金属球甲、乙分别浸没在左右两液体中,均无液体溢出,此时A点的压强大于B点的压强,则一定成立的是( )
(2013?太仓市模拟)如图所示,两个底面积不同的圆柱形容器内分别盛有深度不同的液体,已知距容器底部均为h的A、B两点的压强相等.现将实心金属球甲、乙分别浸没在左右两液体中,均无液体溢出,此时A点的压强大于B点的压强,则一定成立的是( ) 如图所示,两个底面积不同的圆柱形容器甲和乙,容器足够高,分别盛有质量相等的水和酒精(ρ水>ρ酒精),可能使水和酒精对容器底部的压强相等的方法是
如图所示,两个底面积不同的圆柱形容器甲和乙,容器足够高,分别盛有质量相等的水和酒精(ρ水>ρ酒精),可能使水和酒精对容器底部的压强相等的方法是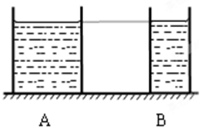 如图所示,两个底面积不同的圆柱形容器A和B内装有同种液体,液面高度相同.液体对各自容器底部的压强PA、PB 和压力FA、FB的关系是PA
如图所示,两个底面积不同的圆柱形容器A和B内装有同种液体,液面高度相同.液体对各自容器底部的压强PA、PB 和压力FA、FB的关系是PA