题目内容
一个人站在河边,能看见河对岸一颗在水中的像.当人从河岸后退6m时,恰好就不能看到整个树我像了,已知人身高1.5m,河岸高出水面1cm,河宽40m,求树有多高?
根据题意画出图形,在直角△COB′、△OGH和△GFF′相似,则每个三角形的直角边之比为一定值,则: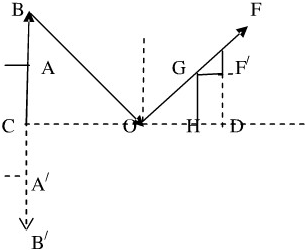
=
=
又GF′=6m,FF′=1.5m,GH=1m
则
=
即OH=4m
而CO=40m-4m=36m
又因为
=4所以 CB′=
CO=
×36m=9m
故AB=A′B′=CB′-CA′=9m-1m=8m
答:树高为8m.

| CO |
| CB′ |
| OH |
| GH |
| GF′ |
| FF′ |
则
| OH |
| 1 |
| 6 |
| 1.5 |
而CO=40m-4m=36m
又因为
| CO |
| CB′ |
| 1 |
| 4 |
| 1 |
| 4 |
故AB=A′B′=CB′-CA′=9m-1m=8m
答:树高为8m.

练习册系列答案
相关题目