题目内容
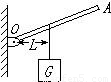
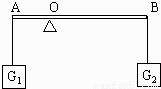 如图所示的轻质杠杆,AO 小于 BO.在 A、B 两端悬挂重物 G1 和 G2后杠杆 平衡,若将 G1 和 G2 同时向支点 O 移动相同的距离,则( )
如图所示的轻质杠杆,AO 小于 BO.在 A、B 两端悬挂重物 G1 和 G2后杠杆 平衡,若将 G1 和 G2 同时向支点 O 移动相同的距离,则( )A.杠杆仍保持平衡
B.杠杆的A端向下倾斜
C.杠杆的B端向下倾斜
D.无法判断
【答案】分析:杠杆原来处于平衡状态,利用图示杠杆的力臂大小关系,根据杠杆平衡条件得到物体A、B的质量大小关系;
利用现在的力臂和力分别表示出杠杆作用两边的力矩:力和力臂的乘积.比较力矩的大小,即可确定杠杆是否平衡.
解答:解:原来杠杆在水平位置处于平衡状态,此时作用在杠杆上的力分别为G1和G2,其对应的力臂分别为OA、OB,
根据杠杆的平衡条件可得:G1?OA=G2?OB,由图示可知,OA<OB.所以:G1>G2,
当向支点移动相同的距离△L时,两边的力臂都减小△L,此时左边的力矩为:G1(OA-△L)=G1OA-G1△L,
右边的力矩为:G2(OB-△L)=G2OB-G2△L,由于G1>G2,所以G1△L>G2△L;
所以:G1OA-G1△L<G2OB-G2△L,
因此杠杆将向右端倾斜.
综上分析故选C.
点评:根据杠杆第一次处于平衡状态,利用杠杆的平衡条件,确定G1和G2,大小关系;然后根据现在作用在杠杆上的力和力臂表示出两者力矩,利用推导出物体的重力关系,和力臂关系,得出两个力矩的大小关系,从而确定杠杆的偏转方向.这是此题的解题思路.
利用现在的力臂和力分别表示出杠杆作用两边的力矩:力和力臂的乘积.比较力矩的大小,即可确定杠杆是否平衡.
解答:解:原来杠杆在水平位置处于平衡状态,此时作用在杠杆上的力分别为G1和G2,其对应的力臂分别为OA、OB,
根据杠杆的平衡条件可得:G1?OA=G2?OB,由图示可知,OA<OB.所以:G1>G2,
当向支点移动相同的距离△L时,两边的力臂都减小△L,此时左边的力矩为:G1(OA-△L)=G1OA-G1△L,
右边的力矩为:G2(OB-△L)=G2OB-G2△L,由于G1>G2,所以G1△L>G2△L;
所以:G1OA-G1△L<G2OB-G2△L,
因此杠杆将向右端倾斜.
综上分析故选C.
点评:根据杠杆第一次处于平衡状态,利用杠杆的平衡条件,确定G1和G2,大小关系;然后根据现在作用在杠杆上的力和力臂表示出两者力矩,利用推导出物体的重力关系,和力臂关系,得出两个力矩的大小关系,从而确定杠杆的偏转方向.这是此题的解题思路.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 7、如图所示的轻质杠杆,AO<BO,在A、B处分别悬挂重物G1和G2时杠杆处于平衡.若将G1和G2同时向外运动相同的距离,则( )
7、如图所示的轻质杠杆,AO<BO,在A、B处分别悬挂重物G1和G2时杠杆处于平衡.若将G1和G2同时向外运动相同的距离,则( )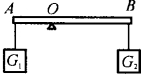 2、如图所示的轻质杠杆,AO小于BO.在A、B两端悬挂重物G1和G2后杠杆平衡.若将G1和G2同时向支点O移动相同的距离,则杠杆
2、如图所示的轻质杠杆,AO小于BO.在A、B两端悬挂重物G1和G2后杠杆平衡.若将G1和G2同时向支点O移动相同的距离,则杠杆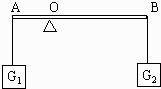 (2003?天津)如图所示的轻质杠杆,AO 小于 BO.在 A、B 两端悬挂重物 G1 和 G2后杠杆 平衡,若将 G1 和 G2 同时向支点 O 移动相同的距离,则( )
(2003?天津)如图所示的轻质杠杆,AO 小于 BO.在 A、B 两端悬挂重物 G1 和 G2后杠杆 平衡,若将 G1 和 G2 同时向支点 O 移动相同的距离,则( )