题目内容
甲乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点相遇,如图所示.已知甲的速度是5m/s,乙的速度是3m/s,跑道上OC段长度为60m.如果他们从A点同时都沿A-B-C-D同向绕行,至少要经多长时间才能相遇?在什么地方相遇?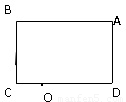
【答案】分析:当甲乙二人反向绕行时,在O点相遇,设跑到周长为S,甲运动的路程为 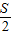 +60m,乙运动的路程为
+60m,乙运动的路程为 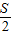 -60m,根据速度公式求所用时间,根据所用时间相同列方程求解;
-60m,根据速度公式求所用时间,根据所用时间相同列方程求解;
甲、乙两人从同一点同时出发沿同方向在跑道上绕行,当他们在同一地点再次相遇时,甲比乙多跑一圈,设所用时间为t,列出关于t的方程求解.再求出乙所跑路程确定相遇位置.
解答:解:设跑道周长为S,反向绕行时,
甲运动的路程为:s甲=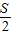 +60m,-----①
+60m,-----①
乙运动的路程为:s乙=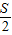 -60m,-----②
-60m,-----②
由于相遇时运动的时间相等,则:
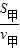 =
=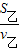 ,
,
即: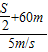 =
=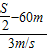 ,
,
解得:
S=480m;
设设同向绕行时ts后相遇,
由题知,s甲=s乙+480m,
∵v= ,v甲=5m/s、v乙=3m/s,
,v甲=5m/s、v乙=3m/s,
∴5m/s×t=3m/s×t+480m,
解得:t=240s,
s乙=v乙t=3m/s×240s=720m,
相遇地点与起点A的距离为:s′乙-s=720m-480m=240m,即在C点相遇.
答:至少经240s后才能相遇,在C点相遇.
点评:本题考查了速度公式的应用,本题关键:一是确定无论是同向还是反向绕行,相遇时用的时间相同;二是确定同向和反向绕行时二人所跑路程的关系.
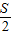 +60m,乙运动的路程为
+60m,乙运动的路程为 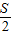 -60m,根据速度公式求所用时间,根据所用时间相同列方程求解;
-60m,根据速度公式求所用时间,根据所用时间相同列方程求解;甲、乙两人从同一点同时出发沿同方向在跑道上绕行,当他们在同一地点再次相遇时,甲比乙多跑一圈,设所用时间为t,列出关于t的方程求解.再求出乙所跑路程确定相遇位置.
解答:解:设跑道周长为S,反向绕行时,
甲运动的路程为:s甲=
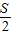 +60m,-----①
+60m,-----①乙运动的路程为:s乙=
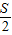 -60m,-----②
-60m,-----②由于相遇时运动的时间相等,则:
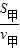 =
=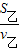 ,
,即:
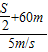 =
= ,
,解得:
S=480m;
设设同向绕行时ts后相遇,
由题知,s甲=s乙+480m,
∵v=
 ,v甲=5m/s、v乙=3m/s,
,v甲=5m/s、v乙=3m/s,∴5m/s×t=3m/s×t+480m,
解得:t=240s,
s乙=v乙t=3m/s×240s=720m,
相遇地点与起点A的距离为:s′乙-s=720m-480m=240m,即在C点相遇.
答:至少经240s后才能相遇,在C点相遇.
点评:本题考查了速度公式的应用,本题关键:一是确定无论是同向还是反向绕行,相遇时用的时间相同;二是确定同向和反向绕行时二人所跑路程的关系.

练习册系列答案
相关题目
 (2013?荆门)甲、乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点相遇,如图所示,已知甲的速度为5m/s,乙的速度为3m/s,跑道OC段长度为50m,如果他们从A点同时开始都沿A→B→C→D同向绕行,则再一次相遇的时间是
(2013?荆门)甲、乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点相遇,如图所示,已知甲的速度为5m/s,乙的速度为3m/s,跑道OC段长度为50m,如果他们从A点同时开始都沿A→B→C→D同向绕行,则再一次相遇的时间是 甲乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点相遇,如图所示.已知甲的速度是5m/s,乙的速度是3m/s,跑道上OC段长度为60m.如果他们从A点同时都沿A-B-C-D同向绕行,至少要经多长时间才能相遇?在什么地方相遇?
甲乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点相遇,如图所示.已知甲的速度是5m/s,乙的速度是3m/s,跑道上OC段长度为60m.如果他们从A点同时都沿A-B-C-D同向绕行,至少要经多长时间才能相遇?在什么地方相遇? 甲、乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点第一次相遇,如图所示,已知甲的速度为5m/s,乙的速度为3m/s,跑道OC段长度为50m,两人经过
甲、乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点第一次相遇,如图所示,已知甲的速度为5m/s,乙的速度为3m/s,跑道OC段长度为50m,两人经过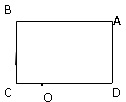 甲乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点相遇,如图所示.已知甲的速度是5m/s,乙的速度是3m/s,跑道上OC段长度为60m.如果他们从A点同时都沿A-B-C-D同向绕行,至少要经多长时间才能相遇?在什么地方相遇?
甲乙两人从矩形跑道的A点同时开始沿相反方向绕行,在O点相遇,如图所示.已知甲的速度是5m/s,乙的速度是3m/s,跑道上OC段长度为60m.如果他们从A点同时都沿A-B-C-D同向绕行,至少要经多长时间才能相遇?在什么地方相遇?