题目内容
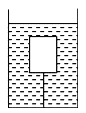
【题目】如图所示,体积为1000cm3的长方体木块浸没在底面积为200 cm2装有水的柱形容器中,此时水的深度为20cm.剪断细线后木块露出水面2/5(取g=10N/kg)求:
(1)细线末断时水对容器底的压强.
(2)木块的密度
(3)细线末断时细线的拉力
(4)剪断细线前后水对容器底压强的变化量。
【答案】2000 Pa 0.6×103kg/m3 4 N 200 Pa
【解析】(1)由题知,容器中的水深度为20cm,此时容器底部所受水的压强:
p=ρ水 gh=1.0×103 kg/m3 ×10N/kg×0.2m=2000Pa;
(2)剪断细线后木块漂浮,且有2/5露出水面,此时F浮 =G木 ,
由阿基米德原理和密度公式有:ρ水 V排 g=ρ木 V木 g,
木块密度;ρ木 =V排ρ水/V木 =(V木2V木/5 )ρ水/V木=0.6×103 kg/m3 ;
(3)木块重力:G木 =ρ木 V木 g=0.6×103 kg/m3 ×1000×10-6 m3×10N/kg=6N,木块浸没时的浮力:F浮 =ρ水 gV排 =1.0×103 kg/m3 ×10N/kg×1000×10-6m3 =10N,木块处于静止状态,受到的浮力、重力和绳子拉力平衡,所以:F浮 =G木 +F,所以细线的拉力:F=F浮 -G木 =10N-6N=4N;
(4)剪断细线后木块漂浮,排开水的体积减小,水面下降,△V=V露 =S△h,即:2 V木 /5=S△h,所以:△h=2 V木/5 S=2/5×10003/200cm2=2cm,
所以剪断细线前后水对容器底压强的变化量:
△p=ρ水 g△h=1.0×103 kg/m3 ×10N/kg×0.02m=200Pa

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目