题目内容
阅读短文,回答文后问题孔明灯
我国汉代曾发明过一种用做军事信号的“孔明灯”,它其实就是一种灯笼.先用很轻的竹篾扎成框架,再用纸糊严,并在下面留口.在灯笼的下面固定一个小碟,在碟内放入燃料.点燃后,当灯笼内的空气被加热到一定温度时,灯笼就能腾空而起.灯笼受到的空气浮力可以用阿基米德原理计算,即F浮=ρ空气gV (本题g取10N/kg).温度为20℃时,空气密度为1.2kg/m3,下表给出了一些空气密度和温度的对应关系.
| 温度/℃ | 90 | 100 | 110 | 120 | 130 |
| 密度/kg?m-3 | 0.97 | 0.94 | 0.91 | 0.88 | 0.85 |
A.质量 B.密度 C.热值 D.比热容
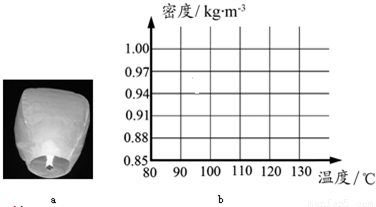
(2)根据表格中的数据,在坐标图中作出空气密度和温度关系的图象.
(3)如图a所示的孔明灯体积大约为0.02m3,环境气温为20℃,则孔明灯受到的空气浮力为______N.
(4)上题中孔明灯制作材料和燃料总质量为6g,灯内空气的温度要达到______℃,孔明灯才能起飞(忽略燃料质量的变化).
【答案】分析:(1)孔明灯要飞起来,需要利用空气的浮力克服自身的重力,所以燃料应该尽量减轻质量.
(2)根据表格中的数据,在坐标系中找出密度和温度的对应点,按照数学上的描点连线方法完成作图.
(3)已知20℃的空气密度和孔明灯的体积,利用F浮=ρgV计算孔明灯在空气中受到的浮力.
(4)孔明灯飞起时,受到三个力的作用:空气的浮力、灯的重力、灯内热空气的重力,且浮力为两个重力之和,据此得到热空气的重力;已知热空气的重力和孔明灯的体积,利用ρ=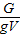 得到热空气的密度,将热空气的密度与密度与温度对应关系进行比较,确定热空气达到的温度.
得到热空气的密度,将热空气的密度与密度与温度对应关系进行比较,确定热空气达到的温度.
解答:解:
(1)为保证孔明灯更容易起飞,燃料的质量在保证飞行时间的前提下尽可能地减小;
故答案为:A;
(2)空气密度与温度对应关系图象如图所示:
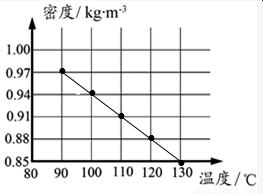
(3)孔明灯在空气中受到的浮力为F浮=ρ空气gV=1.2kg/m3×10N/kg×0.02m3=0.24N;
故答案为:0.24;
(4)当孔明灯浮起时,说明受到的空气浮力刚好等于灯重与灯内热空气重力之和.
即F浮=G灯+G热
0.24N=0.006kg×10N/kg+G热
0.18N=ρ热gV
ρ热=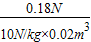 =0.9kg/m3
=0.9kg/m3
由空气密度和温度的对应关系知,在110~120℃之间,温度升高10℃,空气密度减小0.03kg/m3
此时的空气密度为0.9kg/m3,较0.91kg/m3减小0.01kg/m3,所以温度升高接近3℃,即此时的温度约为113℃.
故答案为:113.
点评:第四小题难度较大,突破的关键是根据孔明灯浮起时受到的浮力与两个重力合力为零,据此列出等量关系式,然后读懂空气密度与温度之间的变化规律,便能求解.
(2)根据表格中的数据,在坐标系中找出密度和温度的对应点,按照数学上的描点连线方法完成作图.
(3)已知20℃的空气密度和孔明灯的体积,利用F浮=ρgV计算孔明灯在空气中受到的浮力.
(4)孔明灯飞起时,受到三个力的作用:空气的浮力、灯的重力、灯内热空气的重力,且浮力为两个重力之和,据此得到热空气的重力;已知热空气的重力和孔明灯的体积,利用ρ=
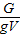 得到热空气的密度,将热空气的密度与密度与温度对应关系进行比较,确定热空气达到的温度.
得到热空气的密度,将热空气的密度与密度与温度对应关系进行比较,确定热空气达到的温度.解答:解:
(1)为保证孔明灯更容易起飞,燃料的质量在保证飞行时间的前提下尽可能地减小;
故答案为:A;
(2)空气密度与温度对应关系图象如图所示:

(3)孔明灯在空气中受到的浮力为F浮=ρ空气gV=1.2kg/m3×10N/kg×0.02m3=0.24N;
故答案为:0.24;
(4)当孔明灯浮起时,说明受到的空气浮力刚好等于灯重与灯内热空气重力之和.
即F浮=G灯+G热
0.24N=0.006kg×10N/kg+G热
0.18N=ρ热gV
ρ热=
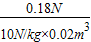 =0.9kg/m3
=0.9kg/m3由空气密度和温度的对应关系知,在110~120℃之间,温度升高10℃,空气密度减小0.03kg/m3
此时的空气密度为0.9kg/m3,较0.91kg/m3减小0.01kg/m3,所以温度升高接近3℃,即此时的温度约为113℃.
故答案为:113.
点评:第四小题难度较大,突破的关键是根据孔明灯浮起时受到的浮力与两个重力合力为零,据此列出等量关系式,然后读懂空气密度与温度之间的变化规律,便能求解.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目