题目内容
 一个半径为5m的圆形蓄水池装满水,水面和地面相平,在池中心正上方离水面3m高处吊着一盏灯,一个人站在岸边,他的眼睛距地面的高度为1.8m,则他要看到灯在水中所成的像,人到岸的距离不能超过( )
一个半径为5m的圆形蓄水池装满水,水面和地面相平,在池中心正上方离水面3m高处吊着一盏灯,一个人站在岸边,他的眼睛距地面的高度为1.8m,则他要看到灯在水中所成的像,人到岸的距离不能超过( )A.1m
B.2m
C.3m
D.4m
【答案】分析:(1)当人的眼睛看到灯的像时,人的眼睛和像在同一直线上;
(2)当人的眼睛,池子的边缘、灯在水中的像点在同一直线上时,此时人距离池子的距离最远,再远人就看不到灯在水中的像了,由此入手确定人到池子的最远距离.
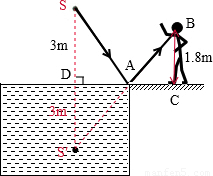
解答:解:(1)根据平面镜成像的规律:像与物关于镜面对称,以水面为平面镜做出灯S在水中的像S′,因为SD=3m,所以S′D=3m.
(2)连接S′A并延长至人的眼睛,如下图所示,BC为人眼睛到地面的距离,AC为人到池子的距离.
(3)由题意可知,DS′=3m,DA=5m,BC=1.8m,两个直角三角形:△DAS′与△CAB相似.
相似形的对应边成比例,所以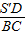 =
=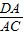 ;
;
人到池子的最远距离:AC=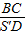 DA=
DA=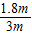 ×5m=3m.
×5m=3m.
故选C.
点评:(1)此题考查了平面镜成像的规律、相似形的特点、光沿直线传播.
(2)根据平面镜成像的规律做出其成像的位置,利用光沿直线传播确定人看到像的最远位置是解决此题的关键.
(2)当人的眼睛,池子的边缘、灯在水中的像点在同一直线上时,此时人距离池子的距离最远,再远人就看不到灯在水中的像了,由此入手确定人到池子的最远距离.
解答:解:(1)根据平面镜成像的规律:像与物关于镜面对称,以水面为平面镜做出灯S在水中的像S′,因为SD=3m,所以S′D=3m.
(2)连接S′A并延长至人的眼睛,如下图所示,BC为人眼睛到地面的距离,AC为人到池子的距离.
(3)由题意可知,DS′=3m,DA=5m,BC=1.8m,两个直角三角形:△DAS′与△CAB相似.
相似形的对应边成比例,所以
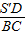 =
=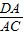 ;
;人到池子的最远距离:AC=
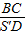 DA=
DA=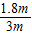 ×5m=3m.
×5m=3m.
故选C.
点评:(1)此题考查了平面镜成像的规律、相似形的特点、光沿直线传播.
(2)根据平面镜成像的规律做出其成像的位置,利用光沿直线传播确定人看到像的最远位置是解决此题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 (2012?黄石)一个半径为5m的圆形蓄水池装满水,水面和地面相平,在池中心正上方离水面3m高处吊着一盏灯,一个人站在岸边,他的眼睛距地面的高度为1.8m,则他要看到灯在水中所成的像,人到岸的距离不能超过( )
(2012?黄石)一个半径为5m的圆形蓄水池装满水,水面和地面相平,在池中心正上方离水面3m高处吊着一盏灯,一个人站在岸边,他的眼睛距地面的高度为1.8m,则他要看到灯在水中所成的像,人到岸的距离不能超过( )
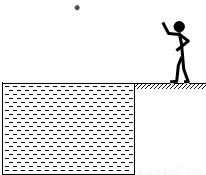 一个半径为5m的圆形蓄水池装满水,水面和地面相平,在池中心正上方离水面3m高处吊着一盏灯,一个人站在岸边,他的眼睛距地面的高度为1.8m,则他要看到灯在水中所成的像,人到岸的距离不能超过( )
一个半径为5m的圆形蓄水池装满水,水面和地面相平,在池中心正上方离水面3m高处吊着一盏灯,一个人站在岸边,他的眼睛距地面的高度为1.8m,则他要看到灯在水中所成的像,人到岸的距离不能超过( ) 一个半径为5m的圆形蓄水池装满水,水面和地面相平,在池中心正上方离水面3m高处吊着一盏灯,一个人站在岸边,他的眼睛距地面的高度为1.8m,则他要看到灯在水中所成的像,人到岸的距离不能超过( )
一个半径为5m的圆形蓄水池装满水,水面和地面相平,在池中心正上方离水面3m高处吊着一盏灯,一个人站在岸边,他的眼睛距地面的高度为1.8m,则他要看到灯在水中所成的像,人到岸的距离不能超过( )