题目内容
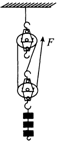 (2012?盘锦)如图所示,为“测量滑轮组机械效率”的实验装置,钩码总质量为0.6kg,小明用2.4N的拉力竖直向上匀速拉动细绳(绳重和摩擦忽略不计,g取10N/kg).
(2012?盘锦)如图所示,为“测量滑轮组机械效率”的实验装置,钩码总质量为0.6kg,小明用2.4N的拉力竖直向上匀速拉动细绳(绳重和摩擦忽略不计,g取10N/kg).(1)若钩码2s内上升0.1m,则钩码上升的速度为多少?
(2)小明拉力做功的功率的是多少?该滑轮组的机械效率是多少?(结果保留一位小数)
(3)当钩码总重力为12N时,该滑轮组的机械效率为多大?(结果保留一位小数).
分析:(1)知道此时钩码上升的高度和上升的时间,据公式V=
可计算出此时钩码上升的速度.
(2)由滑轮组结构得出承担物重的绳子股数n=3,则s=3h,利用W总=Fs求拉力做功,再利用功率公式求拉力做功功率;
先计算出钩码的重力,而后据W有用=Gh计算出有用功,再据上面所计算的总功结合机械效率的计算公式即可计算出此时的机械效率.
(3)据钩码的重力和绳子自由端的拉力可计算出动滑轮的重力,由于该题中绳重和摩擦忽略不计,所以对动滑轮所做的功是额外功,对钩码做的功是有用功,故据额外功和有用功可计算出总功,进而可计算出此时的机械效率.
| S |
| t |
(2)由滑轮组结构得出承担物重的绳子股数n=3,则s=3h,利用W总=Fs求拉力做功,再利用功率公式求拉力做功功率;
先计算出钩码的重力,而后据W有用=Gh计算出有用功,再据上面所计算的总功结合机械效率的计算公式即可计算出此时的机械效率.
(3)据钩码的重力和绳子自由端的拉力可计算出动滑轮的重力,由于该题中绳重和摩擦忽略不计,所以对动滑轮所做的功是额外功,对钩码做的功是有用功,故据额外功和有用功可计算出总功,进而可计算出此时的机械效率.
解答:解:(1)钩码在2s内上升0.1m,故钩码上升的速度为V=
=
=0.05m/s;
(2)由滑轮组结构得出承担物重的绳子股数n=3,则s=3h=3×0.1m=0.3m;
此时拉力做的功是:W总=FS=2.4N×0.3m=0.72J;
故此时的功率是:P=
=
=0.36W;
此时钩码的重力是:G=mg=0.6kg×10N/kg=6N;
故有用功是:W有=FS=Gh=6N×0.1m=0.6J
故此时的机械效率是:η=
=
×100%=83.3%.
(3)在不计绳重和摩擦的情况下,动滑轮的重力是:
G动=nF-G=3×2.4N-6N=1.2N;
假设钩码上升的高度是hm,所以当钩码总重力为12N时的有用功是:W有=FS=Gh=12N×hm=12hJ
此时动滑轮上升的高度是hm,故额外功是:W额=FS=G动h=1.2N×hm=1.2hJ
所以总功是:W总=W有+W额=12hJ+1.2hJ=13.2hJ;
故此时的机械效率是:η=
=
×100%=90.9%.
答:(1)若钩码2s内上升0.1m,则钩码上升的速度为0.05m/s;(2)小明拉力做功的功率0.36W;该滑轮组的机械效率是83.3%;(3)当钩码总重力为12N时,该滑轮组的机械效率90.9%.
| S |
| t |
| 0.1m |
| 2s |
(2)由滑轮组结构得出承担物重的绳子股数n=3,则s=3h=3×0.1m=0.3m;
此时拉力做的功是:W总=FS=2.4N×0.3m=0.72J;
故此时的功率是:P=
| W |
| t |
| 0.72J |
| 2s |
此时钩码的重力是:G=mg=0.6kg×10N/kg=6N;
故有用功是:W有=FS=Gh=6N×0.1m=0.6J
故此时的机械效率是:η=
| W有 |
| W总 |
| 0.6J |
| 0.72J |
(3)在不计绳重和摩擦的情况下,动滑轮的重力是:
G动=nF-G=3×2.4N-6N=1.2N;
假设钩码上升的高度是hm,所以当钩码总重力为12N时的有用功是:W有=FS=Gh=12N×hm=12hJ
此时动滑轮上升的高度是hm,故额外功是:W额=FS=G动h=1.2N×hm=1.2hJ
所以总功是:W总=W有+W额=12hJ+1.2hJ=13.2hJ;
故此时的机械效率是:η=
| W有 |
| W总 |
| 12hJ |
| 13.2hJ |
答:(1)若钩码2s内上升0.1m,则钩码上升的速度为0.05m/s;(2)小明拉力做功的功率0.36W;该滑轮组的机械效率是83.3%;(3)当钩码总重力为12N时,该滑轮组的机械效率90.9%.
点评:该题考查了速度、功率、机械效率的计算,能理清题意,并能看出该题中的动滑轮的自身重不变是解决该题的关键.

练习册系列答案
相关题目
 (2012?盘锦)如图所示为小球在地面弹跳的频闪照片.根据此图,以下分析正确的是( )
(2012?盘锦)如图所示为小球在地面弹跳的频闪照片.根据此图,以下分析正确的是( )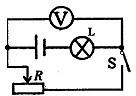 (2012?盘锦)如图所示,电源电压恒定不变,滑动变阻器的滑片向右移动过程中,下列说法正确的是( )
(2012?盘锦)如图所示,电源电压恒定不变,滑动变阻器的滑片向右移动过程中,下列说法正确的是( )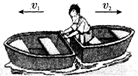 (2012?盘锦)如图所示,两只小船静止在水面上,小明用力推另一只小船,另一只小船会向前运动,说明力可以改变物体的
(2012?盘锦)如图所示,两只小船静止在水面上,小明用力推另一只小船,另一只小船会向前运动,说明力可以改变物体的 (2012?盘锦)如图甲所示,用吸管把饮料吸进嘴里,是靠
(2012?盘锦)如图甲所示,用吸管把饮料吸进嘴里,是靠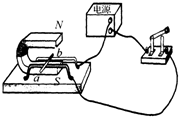 (2012?盘锦)如图所示,把导线ab(开关断开)放在磁场里,导线ab
(2012?盘锦)如图所示,把导线ab(开关断开)放在磁场里,导线ab