题目内容
【题目】某地区道路如图所示,歹徒在A处作案后沿AB以5m/s的速度逃跑,到达B时停留1s接着沿BC以6m/s速度逃跑,在歹徒经过AB中点时,被见义勇为的小明同学发现,并立即从A出发,沿AC拦截歹徒,结果警方和他恰好在C处将歹徒抓获.
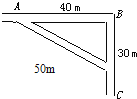
(1)歹徒从被发现至C处被捕共历时多少s?
(2)小明追捕歹徒的速度为多少m/s,合多少km/h.
【答案】(1)10s;
(2)5m/s,合18km/h.
【解析】已知:歹徒从被发现到B点的距离s1=![]() sAB=
sAB=![]() ×40m=20m,沿AB的逃跑速度v1=5m/s,sBC=30m,沿BC的逃跑速度v2=6m/s,停留时间t3=1s
×40m=20m,沿AB的逃跑速度v1=5m/s,sBC=30m,沿BC的逃跑速度v2=6m/s,停留时间t3=1s
求:(1)歹徒从被发现至C处被捕的时间t=?;(2)小明追捕歹徒的速度v=?
解:(1)∵v=![]() ,
,
∴歹徒从被发现到B点的时间:
t1=![]() =
=![]() =4s,
=4s,
沿BC的逃跑时间:
t2=![]() =
=![]() =5s,
=5s,
歹徒从被发现至C处被捕的时间:
t=t1+t2+t3=4s+5s+1s=10s;
(2)小明追捕歹徒的时间等于歹徒从被发现至C处被捕的时间,
由几何知识可知:sAC=![]() =
=![]() =50m,
=50m,
小明追捕歹徒的速度:
v=![]() =
=![]() =5m/s=18km/h.
=5m/s=18km/h.
答:(1)歹徒从被发现至C处被捕的时间为10s;
(2)小明追捕歹徒的速度为5m/s,合18km/h.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目