题目内容
一静水湖的南北两岸,有两只船同时相向开出,各以其速度垂直于湖岸匀速驶向对岸.两船在离北岸800米处迎面相会,相会后继续驶向对岸.靠岸后立即返航,两船又在离南岸600米处迎面相会.若不计两船靠岸时间,求湖宽.
解法一:湖宽为s米,从北岸出发的船行驶速度为v1,从南岸出发的船行驶速度为v2,两船第一次相会,行驶时间相等,依据题意有
 =
=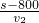 ①
①
两船第二次相会,行驶时间也相等,依据题意有
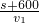 =
= ②
②
联立①式和②式,解得:s=1800m.
答:湖宽为1800米.
解法二:根据题意可知,两船第一次相会时,两船通过的路程之和为湖宽s,此时从北岸出发的船通过的路程为800米.两船第二次相会时,两船通过的路程之和是3s,从北岸出发的船通过的路程为(s+600)米.根据路程之比等于速度之比,则有
 =
=
解得:s=1800米
答:湖宽为1800米.
分析:解法一:两船从出发到到相遇,行驶的时间相等,分别列出第一次相遇、第二次相遇的时间相等关系式,解方程得到湖宽s;
解法二:根据路程之比等于速度之比,列出比例关系式,求出湖宽s.
点评:本题的联系点是两船运动的时间始终相等,用到比例式: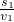 =
=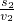 、
、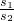 =
=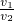 .
.
 =
=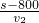 ①
①两船第二次相会,行驶时间也相等,依据题意有
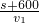 =
= ②
②联立①式和②式,解得:s=1800m.
答:湖宽为1800米.
解法二:根据题意可知,两船第一次相会时,两船通过的路程之和为湖宽s,此时从北岸出发的船通过的路程为800米.两船第二次相会时,两船通过的路程之和是3s,从北岸出发的船通过的路程为(s+600)米.根据路程之比等于速度之比,则有
 =
=
解得:s=1800米
答:湖宽为1800米.
分析:解法一:两船从出发到到相遇,行驶的时间相等,分别列出第一次相遇、第二次相遇的时间相等关系式,解方程得到湖宽s;
解法二:根据路程之比等于速度之比,列出比例关系式,求出湖宽s.
点评:本题的联系点是两船运动的时间始终相等,用到比例式:
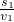 =
=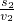 、
、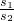 =
=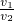 .
. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目