��Ŀ����
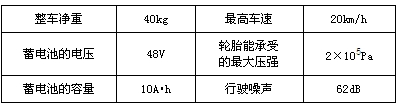
��ͼ��AB�������4km��MN����AB����ƽ�е�һ��С�ӵĺӰ���AB���Ӱ��Ĵ�ֱ����Ϊ3km��С��Ҫ��A���ߵ��Ӱ�ȡˮȻ���͵�B���������ش�ֱ�ںӰ��ķ���D��ȡˮȻ������DB��B������С�����ٶȴ�С��Ϊ5km/h��������ȡˮͣ����ʱ�䡣
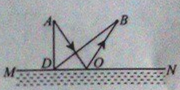
��1����С��������ȡˮ����ˮ��������Ҫ����ʱ�䡣
��2��Ϊ���ҵ�һ�����·�ߣ�����A���Ӱ��ʹӺӰ���B����·����̣������Խ�MN����һ��ƽ�澵����A������һ�����߾�MN�����ǡ��ͨ��B�㣬����֤�������O��Ϊ���·�ߵ�ȡˮ�㡣

��1����С��������ȡˮ����ˮ��������Ҫ����ʱ�䡣
��2��Ϊ���ҵ�һ�����·�ߣ�����A���Ӱ��ʹӺӰ���B����·����̣������Խ�MN����һ��ƽ�澵����A������һ�����߾�MN�����ǡ��ͨ��B�㣬����֤�������O��Ϊ���·�ߵ�ȡˮ�㡣
��1��1.6h(2)������
��1����ͼ��AD=3��AB=4�����ߴ�ֱ������DB=5
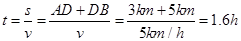
��2����Ϊ������ߵķ����ӳ��߹���㣬����������A�����C,����ƽ�澵������ص㣬������������.
�������MN�ԳƷֲ������AO=CO;
AO+BO=CO+BO=BC
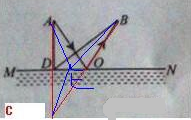
����ѡ��һ��������ȡˮ�����E�㣬��ôȡˮ·�߾���AE+BE����������Գƣ���AE=CE,���������ζ���֮�ʹ��ڵ����ߣ�·��AE+BE=CE+BE>BC
����BC·����̣��������OΪ���·��ȡˮ�㡣
����Ľ�����ѧ֪ʶ����Ҫ��������ѧ�е����������ߴ�С��ϵ��������������������Ĺؼ���
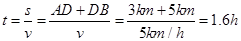
��2����Ϊ������ߵķ����ӳ��߹���㣬����������A�����C,����ƽ�澵������ص㣬������������.
�������MN�ԳƷֲ������AO=CO;
AO+BO=CO+BO=BC

����ѡ��һ��������ȡˮ�����E�㣬��ôȡˮ·�߾���AE+BE����������Գƣ���AE=CE,���������ζ���֮�ʹ��ڵ����ߣ�·��AE+BE=CE+BE>BC
����BC·����̣��������OΪ���·��ȡˮ�㡣
����Ľ�����ѧ֪ʶ����Ҫ��������ѧ�е����������ߴ�С��ϵ��������������������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ



 ��
��