题目内容
 (2012?黄冈)2011年8月我国自主研制的深海探测器--“蛟龙号”(如图1所示)在太平洋海域成功完成5000m深海探测.2012年6月它将再赴马里亚纳海沟挑战7000m深海探测(不考虑海水密度变化,密度ρ取1.0×103kg/m3,g取10N/kg).
(2012?黄冈)2011年8月我国自主研制的深海探测器--“蛟龙号”(如图1所示)在太平洋海域成功完成5000m深海探测.2012年6月它将再赴马里亚纳海沟挑战7000m深海探测(不考虑海水密度变化,密度ρ取1.0×103kg/m3,g取10N/kg).(1)若“蛟龙号”能承受的最大压强是7.2×107Pa,则它能下潜的最大深度是多少?(不考虑大气压)
(2)“蛟龙号”上一面积为50cm2的观测窗口:在上述两种深度的探测中承受的压力增加了多少?
(3)“蛟龙号”完成任务后.漂浮在海面上,由起重装置将其匀速竖直吊离水面,起重装置起吊拉力的功率随时间变化的图象如图2所示,图中P2=2P1.起吊过程中“蛟龙号”总质量为22吨,求t1时刻“蛟龙号”的排水体积(不考虑水的阻力).
分析:(1)知道“蛟龙号”能承受的最大压强,利用公式p=ρgh求能下潜的最大深度;
(2)求出上述两种深度的深度差,利用公式p=ρgh求两种深度的压强差,再利用F=pS求观测窗口在上述两种深度的探测中承受的压力增加值;
(3)设在t1、t2时刻起重装置对探测器的拉力分别为F1、F2,探测器的速度为v,在t1、t2时刻,对探测器进行受力分析,得出F1和F2的大小,而P2=2P1,据此求出t1时刻受到的浮力,再根据阿基米德原理求t1时刻“蛟龙号”的排水体积.
(2)求出上述两种深度的深度差,利用公式p=ρgh求两种深度的压强差,再利用F=pS求观测窗口在上述两种深度的探测中承受的压力增加值;
(3)设在t1、t2时刻起重装置对探测器的拉力分别为F1、F2,探测器的速度为v,在t1、t2时刻,对探测器进行受力分析,得出F1和F2的大小,而P2=2P1,据此求出t1时刻受到的浮力,再根据阿基米德原理求t1时刻“蛟龙号”的排水体积.
解答:解:(1)∵p=ρgh,
能下潜的最大深度:
h=
=
=7200m;
(2)上述两种深度的深度差:
△h=7000m-5000m=2000m,
△p=ρg△h=1×103kg/m3×10N/kg×2000m=2×107Pa,
△F=△pS=2×107Pa×50×10-4m2=1×105N;
(3)设在t1、t2时刻起重装置对探测器的拉力分别为F1、F2,探测器的速度为v,
t1时刻,探测器:F1+F浮=mg,可得F1=mg-F浮,
t2时刻,探测器:F2=mg,
由题知,P2=2P1,
即:F2v=2F1v,
∴F2=2F1,
∴mg=2(mg-F浮)
F浮=
mg=
×22×103kg×10N/kg=1.1×105N,
∵F浮=ρ水V排g,
∴V排=
=
=11m3.
答:(1)“蛟龙号”最大深度是7200m;
(2)在上述两种深度的探测中承受的压力增加了1×105N;
(3)t1时刻“蛟龙号”的排水体积为11m3.
能下潜的最大深度:
h=
| p |
| ρg |
| 7.2×107Pa |
| 1×103kg/m3×10N/kg |
(2)上述两种深度的深度差:
△h=7000m-5000m=2000m,
△p=ρg△h=1×103kg/m3×10N/kg×2000m=2×107Pa,
△F=△pS=2×107Pa×50×10-4m2=1×105N;
(3)设在t1、t2时刻起重装置对探测器的拉力分别为F1、F2,探测器的速度为v,
t1时刻,探测器:F1+F浮=mg,可得F1=mg-F浮,
t2时刻,探测器:F2=mg,
由题知,P2=2P1,
即:F2v=2F1v,
∴F2=2F1,
∴mg=2(mg-F浮)
F浮=
| 1 |
| 2 |
| 1 |
| 2 |
∵F浮=ρ水V排g,
∴V排=
| F浮 |
| ρ水g |
| 1.1×105N |
| 1×103kg/m3×10N/kg |
答:(1)“蛟龙号”最大深度是7200m;
(2)在上述两种深度的探测中承受的压力增加了1×105N;
(3)t1时刻“蛟龙号”的排水体积为11m3.
点评:本题考查了学生对阿基米德原理、液体压强公式和物体的漂浮条件的掌握和运用,难点在第三问,对两个时刻的探测器进行受力分析得出两个时刻的拉力大小是本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 (2012?黄冈模拟)如图是某同学“测量2.5V小灯泡电阻”的实验,实验中电源电压为3V.
(2012?黄冈模拟)如图是某同学“测量2.5V小灯泡电阻”的实验,实验中电源电压为3V. (2012?黄冈模拟)2011年少数民族运动会“独竹漂”比赛中,来自贵州的胡朝贵以21′30的成绩获得了60米直道竞速比赛的冠军,图甲是他参加比赛的情景.其划行所用的力与时间的关系如图乙所示.
(2012?黄冈模拟)2011年少数民族运动会“独竹漂”比赛中,来自贵州的胡朝贵以21′30的成绩获得了60米直道竞速比赛的冠军,图甲是他参加比赛的情景.其划行所用的力与时间的关系如图乙所示.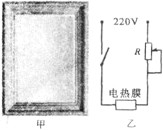 (2012?黄冈模拟)如图甲所示是某型号的浴室防雾镜,其背面粘贴有等大的电热膜.使用时,镜面受热,水蒸气无法凝结其上,便于成像.表是该防雾镜的相关数据.
(2012?黄冈模拟)如图甲所示是某型号的浴室防雾镜,其背面粘贴有等大的电热膜.使用时,镜面受热,水蒸气无法凝结其上,便于成像.表是该防雾镜的相关数据.