题目内容
地面上有一条大木杆,抬起A端需用力300N,抬起B端需用力200N.这条木杆的 端较粗,整个木杆的重量(所受的重力)为 N.
【答案】分析:假设重心在C点,抬A端,以B点为支点;抬B端,以A点为支点.找出两种情况下的动力臂和阻力臂,利用杠杆的平衡条件求木杆重,并且通过比较LAC和LAB的长度得出哪端粗.
解答: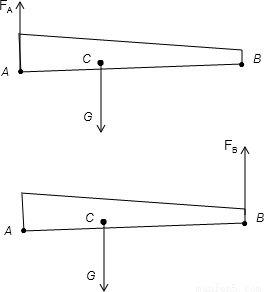 解:如右上图,抬A端,以B点为支点:
解:如右上图,抬A端,以B点为支点:
FALAB=GLBC,--------①
如右上下图,抬B端,以A点为支点:
FBLAB=GLAC,--------②
①+②得:
LAB(FA+FB)=G(LBC+LAC)
∴G=FA+FB=300N+200N=500N
由①得:
LBC=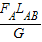 =
= ×LAB=
×LAB= LAB
LAB
由此可知重心C离A端近,A端较粗.
故答案为:A,500.
点评:本题先确定支点,再找出相应的动力和动力臂(动力不同、动力臂相同)、阻力和阻力臂(木杆重不变、力臂不同),利用杠杆的平衡条件列方程组求解.
解答:
 解:如右上图,抬A端,以B点为支点:
解:如右上图,抬A端,以B点为支点:FALAB=GLBC,--------①
如右上下图,抬B端,以A点为支点:
FBLAB=GLAC,--------②
①+②得:
LAB(FA+FB)=G(LBC+LAC)
∴G=FA+FB=300N+200N=500N
由①得:
LBC=
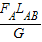 =
= ×LAB=
×LAB= LAB
LAB由此可知重心C离A端近,A端较粗.
故答案为:A,500.
点评:本题先确定支点,再找出相应的动力和动力臂(动力不同、动力臂相同)、阻力和阻力臂(木杆重不变、力臂不同),利用杠杆的平衡条件列方程组求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目